Time-series Classification
Traditional TSC
NN-DTW (Nearest Neighbor coupled with Dynamic Time Warping)
TSC classifier coupled with a distance function - Dynamic Time Warping(DTW) distance used with a NN classifier.
ensemble
ensemble of NN classifiers each with different distance measures outperforms individual NN classifier.
ensemble of decision trees (RandomForest) or ensemble of different types of discriminant classifiers (SVM, 여러가지 distance 방식을 사용하는 NN, 등) 여기에선 times series data를 new feature space로 transform하는 단계가 활용된다. 예를들어, shapelets transform 또는 DTW features를 사용하는 방식, 등
COTE (Collective Of Transformation-based Ensembles)
위 ensemble방식을 기반으로 더 발전된 ensemble임. 35 classifiers로 구성되고, 동일 transformation을 통해 difference classifier들을 ensemble하는 방식이 아니라, instead ensemble different classifiers over difference time representations
HIVE-COTE (COTE with hierarchical vote system)
위 COTE에서 hierarchical vote system과 함께 확장된 방식임. probabilistic voting과 함께 hierarchical structure을 leverage해서 COTE보다 더 개선된 성능이 확보된다. two new classifiers, two additional representation transformation domains가 포함되게 됨. HIVE-COTE는 computationally intensive해서 현실적인 real big data mining 문제에서는 활용되기 어려운것이 단점임. HIVE-COTE는 37 classifiers가 필요하고 algorithm의 hyperparameter의 cross-validating까지 수행되어야함. 예를 들어 37개의 classifier중 하나를 Shapelet Transform을 수행한다면, time complexity가 O(n^2*l^4)수준까지 올라가게됨. (n=number of time series in the dataset, l=length of time series) 또한, HIVE-COTE의 기반이되는 nearest neighbor algorithm이 classification에 많은 시간을 소모한다. 그래서 real-time setting에서는 HIVE-COTE를 적용하기 어렵다.
DNN architecture TSC
Deep learning for time series classification
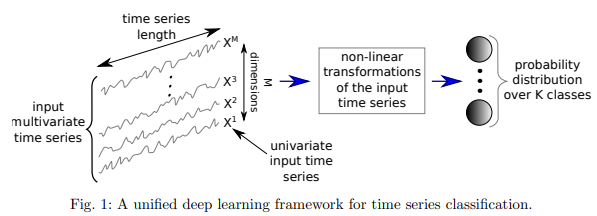
다음 그림과 같이 TSC deep learning framework이 구성된다:
deep learning을 사용하면 특히 multivariate time series data를 다룰때에 문제가 되는 “curse of dimensionality”의 영향을 완화할 수 있다 - by leveraging different degree of smoothness in compositional function as well as the parallel computations of the GPUs 또 다른 장점은 NN-DTW와 같은 non-probabilistic classifier과는 다르게 probabilistic decision이 deep learning network으로 인해 만들어진다는 것이다. algorithm이 제공하는 예측값의 confidence를 가늠할 수 있다.
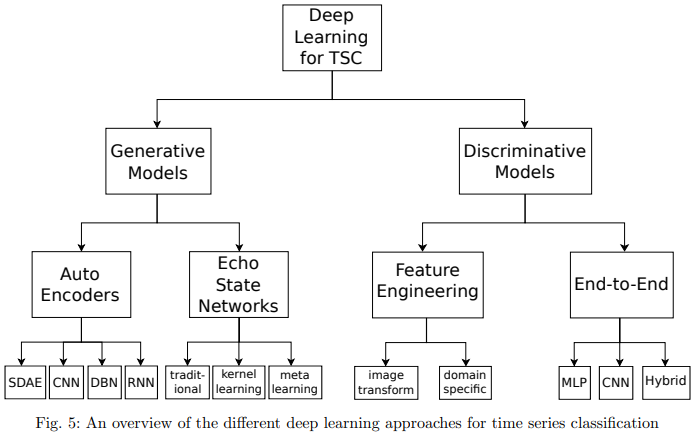
Deep learning TSC의 family overview:
TSC family는 크게 generative와 discriminative model로 나뉜다.
Discriminative model은 directly learns the mapping between raw input of a time series (or its hand engineered features) and outputs a probability distribution over the class variables in a dataset. Distriminative model은 다음과 같이 sub divide 된다:
1) deep learning models with hand engineered features 2) end-to-end deep learning models
end-to-end deep learning model의 경우에는 feature engineering 과정이 필요하지 않은 경우가 많기때문에 domain-specific한 data preprocessing과정이 필수가 아니다.
end-to-end model의 종류로는 MLP, CNN, Hybrid가 있다. MLP의 경우에는 time series data의 temporal information이 lost되기때문에 학습된 features가 충분하지 못한 문제가 있다. CNN의 경우에는 spatially invariant filters (또는 features)를 raw input time series 데이터로부터 추출하고 학습할 수 있다. CNN 기반의 모델 중, 논문의 실험 결과 가장 성능이 높은 architecture로 ResNet, FCN, Encoder가 확인되었다.
FCN(Fully Convolutional Neural Network)
FCN은 local pooling layer없이 convolutional networks로 구성되어있어서 convolution과정동안 time series length가 동일하게 유지된다.
mention된 FCN 모델은 3개의 convolutional blocks로 구성되어있고, 각 block은 3개의 operations를 포함하고있다 - convolution, followed by batch normalization, followed by ReLU activation function.
마지막 convolutional block의 output은 GAP (Global average pooling)구간에 input되어서 time dimension 전체를 기반으로 average된다. 그 다음, softmax classifier를 fully connected network으로 구현하여 모델의 final output을 구한다.
GAP를 활용하기때문에 FCN에서는 “invariance in number of parameters across time series of different lengths”와 같은 장점을 가지고있다. 이 invariance 특성이 있기때문에 transfer learning도 적용 가능하다.
example of FCN:
# source code provided by "Deep Learning for Time Series Classification" repository (https://github.com/hfawaz/dl-4-tsc)
def build_FCN(self, input_shape, nb_classes):
input_layer = keras.layers.Input(input_shape)
conv1 = keras.layers.Conv1D(filters=128, kernel_size=8, padding='same')(input_layer)
conv1 = keras.layers.BatchNormalization()(conv1)
conv1 = keras.layers.Activation(activation='relu')(conv1)
conv2 = keras.layers.Conv1D(filters=256, kernel_size=5, padding='same')(conv1)
conv2 = keras.layers.BatchNormalization()(conv2)
conv2 = keras.layers.Activation('relu')(conv2)
conv3 = keras.layers.Conv1D(128, kernel_size=3,padding='same')(conv2)
conv3 = keras.layers.BatchNormalization()(conv3)
conv3 = keras.layers.Activation('relu')(conv3)
gap_layer = keras.layers.GlobalAveragePooling1D()(conv3)
output_layer = keras.layers.Dense(nb_classes, activation='softmax')(gap_layer)
model = keras.models.Model(inputs=input_layer, outputs=output_layer)
model.compile(loss='categorical_crossentropy', optimizer = keras.optimizers.Adam(),
metrics=['accuracy'])
reduce_lr = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=50,
min_lr=0.0001)
file_path = self.output_directory+'best_model.hdf5'
model_checkpoint = keras.callbacks.ModelCheckpoint(filepath=file_path, monitor='loss',
save_best_only=True)
self.callbacks = [reduce_lr,model_checkpoint]
return model
ResNet
mention된 TSC DL중 가장 deep architecture을 가지고있다. (총 11 layers where first 9 layers are convolutional followed by GAP). ResNet의 주요 특징은 shortcut역할을 하는 residual connection이 convolutional layers 사이에 존재한다는 것이다. 이 shortcut은 linear shortcut으로 residual block의 output을 input과 연결해서 connection을 통해 직접적으로 gradient가 flow되도록 한다. 이런 특징은 vanishing gradient가 발생할 위험을 감소시켜주어서 DL model의 훈련에 더 좋은 영향을 끼친다.
ResNet 모델은 3개의 residual blocks로 구성되어있고 FCN과 비슷하게 GAP layer와 final softmax classifier로 연결 되어있다. 각 residual block은 3개의 convolutions로 구성되어있고, 이들의 output은 residual block의 input으로 더해져서 다음 layer로 flow된다.
ResNet도 FCN과 비슷하게 network 모델이 다른 dataset으로 훈련되었어도 동일한 number of parameters를 가지는 장점을 가지고있다. 그래서 network의 hidden layer의 변경 없이도 transfer learning이 가능하다.
# source code provided by "Deep Learning for Time Series Classification" repository (https://github.com/hfawaz/dl-4-tsc)
def build_model(self, input_shape, nb_classes):
# number of filters for all convolutions is fixed to 64
n_feature_maps = 64
print("input shape: ",input_shape)
print("number of target classes: ",nb_classes)
input_layer = keras.layers.Input(input_shape)
# BLOCK 1 (filter's length(i.e. kernel_size)=8,5,3 for the first, second, third convolutions respectively)
conv_x = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=8, padding='same')(input_layer)
conv_x = keras.layers.BatchNormalization()(conv_x)
conv_x = keras.layers.Activation('relu')(conv_x)
conv_y = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=5, padding='same')(conv_x)
conv_y = keras.layers.BatchNormalization()(conv_y)
conv_y = keras.layers.Activation('relu')(conv_y)
conv_z = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=3, padding='same')(conv_y)
conv_z = keras.layers.BatchNormalization()(conv_z)
# expand channels for the sum
shortcut_y = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=1, padding='same')(input_layer)
shortcut_y = keras.layers.BatchNormalization()(shortcut_y)
output_block_1 = keras.layers.add([shortcut_y, conv_z])
output_block_1 = keras.layers.Activation('relu')(output_block_1)
# BLOCK 2
conv_x = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=8, padding='same')(output_block_1)
conv_x = keras.layers.BatchNormalization()(conv_x)
conv_x = keras.layers.Activation('relu')(conv_x)
conv_y = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=5, padding='same')(conv_x)
conv_y = keras.layers.BatchNormalization()(conv_y)
conv_y = keras.layers.Activation('relu')(conv_y)
conv_z = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=3, padding='same')(conv_y)
conv_z = keras.layers.BatchNormalization()(conv_z)
# expand channels for the sum
shortcut_y = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=1, padding='same')(output_block_1)
shortcut_y = keras.layers.BatchNormalization()(shortcut_y)
output_block_2 = keras.layers.add([shortcut_y, conv_z])
output_block_2 = keras.layers.Activation('relu')(output_block_2)
# BLOCK 3
conv_x = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=8, padding='same')(output_block_2)
conv_x = keras.layers.BatchNormalization()(conv_x)
conv_x = keras.layers.Activation('relu')(conv_x)
conv_y = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=5, padding='same')(conv_x)
conv_y = keras.layers.BatchNormalization()(conv_y)
conv_y = keras.layers.Activation('relu')(conv_y)
conv_z = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=3, padding='same')(conv_y)
conv_z = keras.layers.BatchNormalization()(conv_z)
# no need to expand channels because they are equal
shortcut_y = keras.layers.BatchNormalization()(output_block_2)
output_block_3 = keras.layers.add([shortcut_y, conv_z])
output_block_3 = keras.layers.Activation('relu')(output_block_3)
# FINAL
gap_layer = keras.layers.GlobalAveragePooling1D()(output_block_3)
output_layer = keras.layers.Dense(nb_classes, activation='softmax')(gap_layer)
model = keras.models.Model(inputs=input_layer, outputs=output_layer)
model.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.Adam(),
metrics=['accuracy'])
reduce_lr = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=50, min_lr=0.0001)
file_path = self.output_directory + 'best_model.hdf5'
model_checkpoint = keras.callbacks.ModelCheckpoint(filepath=file_path, monitor='loss',
save_best_only=True)
self.callbacks = [reduce_lr, model_checkpoint]
return model
References
- Deep learning for time series classification: a review(2019) by Hassan Ismail Fawaz, et al (The final authenticated version is available online at: https://doi.org/10.1007/s10618-019-00619-1.)
- Johann Faouzi. Time Series Classification: A review of Algorithms and Implementations. (2022) Machine Learning (Emerging Trends and Applications), In press. ffhal-03558165f