Bayesian Optimization
Bayesian optimization은 위에 해당하는 경우 “블랙박스” 함수를 최적화하는 데 유용한 기술임. “블랙박스” 함수는 입력과 출력 사이의 관계를 알 수 없는 함수를 가르킨다. 예를 들어, 기계 학습 모델의 하이퍼파라미터를 조정하거나, 물리학적 시뮬레이션을 최적화하려는 경우에 해당한다. 이런 경우에는 목적 함수의 값을 직접 계산할 수 없기 때문에, 다양한 입력 값을 시도하고 각각에 대한 출력 값을 측정하는 방법을 사용하여 함수 값을 추정한다.
Bayesian optimization을 통해 Optimal point (e.g., global minima)를 찾는 목표를 달성할 수 있는 case는 다음과 같은 조건을 가진 함수가 주어졌을 때이다:
expensive to compute (만약 computation cost가 매우 낮은 function이라면, 대량의 results를 가지고 grid search를 하는 brute-force 방식을 시도해볼 수 있음.)
problem at hand is a non-convex function,
- is not an analytic expression,
- derivative is now known (많이 사용되는 gradient descent를 사용하려면 derivative를 알아야함.)
Bayesian optimization은 surrogate optimization으로도 불리는데, given sample points를 기반으로 형성된 surrogate 함수를 기반으로 유망한 global minima point를 찾는다. (Surrogate function gives us en estimate of the objective function, which can be used to direct future sampling.) 먼저, given sample points로 측정한 이전 함수 값에 기반하여 함수 값을 추정하고, 추정치의 불확실성을 추적한다. 이를 통해 확률 모델을 만들고, 이 모델을 사용하여 다음에 샘플링할 위치를 결정한다. 이 과정을 반복하면 함수 값을 최소화하는 위치를 찾을 수 있다.
Bayesian statistics의 핵심:
“updating a prior belief in light of new information to produce an updated posterior belief.”
Surrogate 함수는 “probability distribution over possible functions”를 의미하는 Gaussian Processes를 통해 표현될 수 있다. Gaussian process는 training data(evidence)를 기반으로 prior belief를 더 나은 posterior belief로 업데이트 하기때문에, process 그 자체가 Bayesian에 해당된다. (여러 variable들을 대상으로 joint probablity distribution을 만드는 과정은 multivariate Gaussian distribution이라고 함.)
Bayesian optimization에서는 surrogate 함수는 “획득 함수”(acquisition function)를 통해 업데이트 된다. 획득 함수는 exploitation과 exploration 사이의 trade-off를 통해 balance를 유지한다.
exploitation: surrogate model이 good objective를 예측하는 sample을 찾는다. 이미 알려진 유력한 spot을 활용한다. 그러나 만약 이미 탐구했던 지역이라면, 그 지역에서 exploit을 수행하는것은 의미가 없을 것이다.
exploration: 이전에 탐구하지 못한 uncertainty가 높은 지역에서 sample을 찾는다. 전체 영역에서 탐구(explore)되지 못한 지역이 없도록 한 지역에서만 머무르는것을 방지해주는 역할을 맡는다.
획득 함수는 위 두가지 사항의 통해 “최소화하려는 목적 함수”와 “확률 모델의 불확실성” 사이의 균형을 유지하면서 next possible 샘플링 위치를 선택하는 데 사용된다. 획득 함수는 목적 함수를 최소화하는 데 가장 유리한 위치를 찾는 데 중요한 역할을 한다.
Bayesian optimization의 전체적인 과정은 다음과 같이 요약될 수 있다[1].
- Initialize a Gaussian Process ‘surrogate function’ prior distribution.
- Choose several data points x such that the acquisition function a(x) operating on the current prior distribution is maximized.
- Evaluate the data points x in the objective cost function c(x) and obtain the results, y.
- Update the Gaussian Process prior distribution with the new data to produce a posterior (which will become the prior in the next step).
- Repeat steps 2–5 for several iterations.
- Interpret the current Gaussian Process distribution (which is very cheap to do) to find the global minima.
Bayesian optimization을 구현하는 데는 다양한 라이브러리와 도구가 있다. Scikit-Optimize and HyperOpt가 가장 많이 사용됨.
예를 들어, scikit-optimize 라이브러리를 사용하여 Bayesian optimization을 쉽게 구현할 수 있으며, 기계 학습 모델 및 다른 복잡한 함수를 최적화 할 수 있다. 일반적으로 어느정도 잘 작동하는 machine learning model을 validation dataset을 통해 최적화 하는데에 Bayesian optimization을 활용할 수 있다.
Bayesian Optimization in Action
As you iterate over and over, the algorithm balances its needs of exploration and exploitation taking into account what it knows about the target function. At each step a Gaussian Process is fitted to the known samples (points previously explored), and the posterior distribution, combined with a exploration strategy (such as UCB (Upper Confidence Bound), or EI (Expected Improvement)), are used to determine the next point that should be explored (see the gif below).[3]
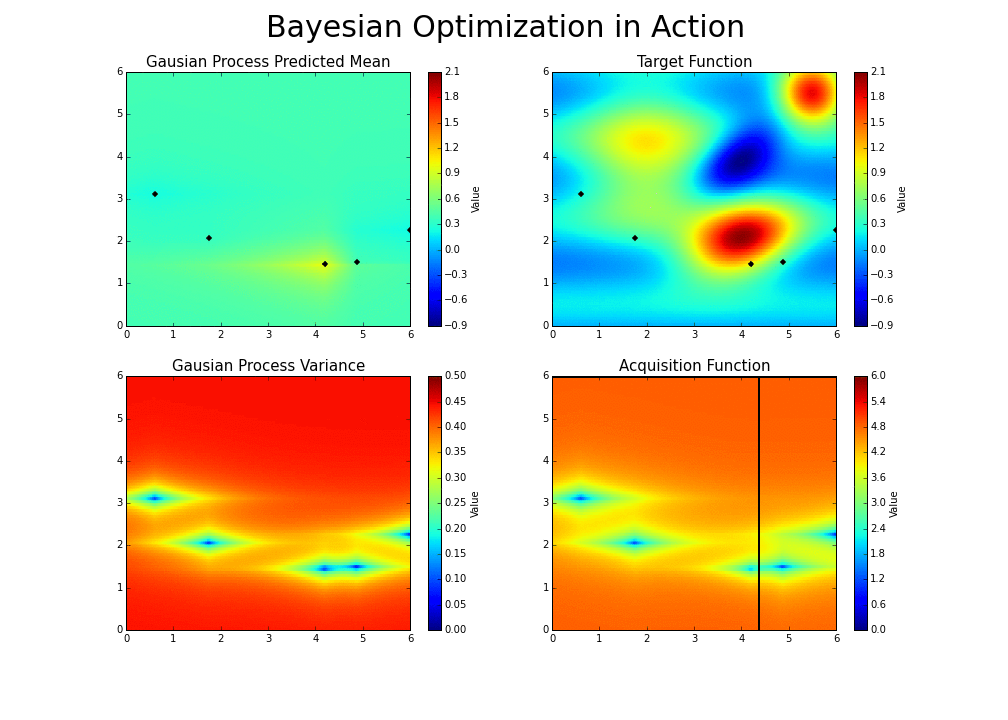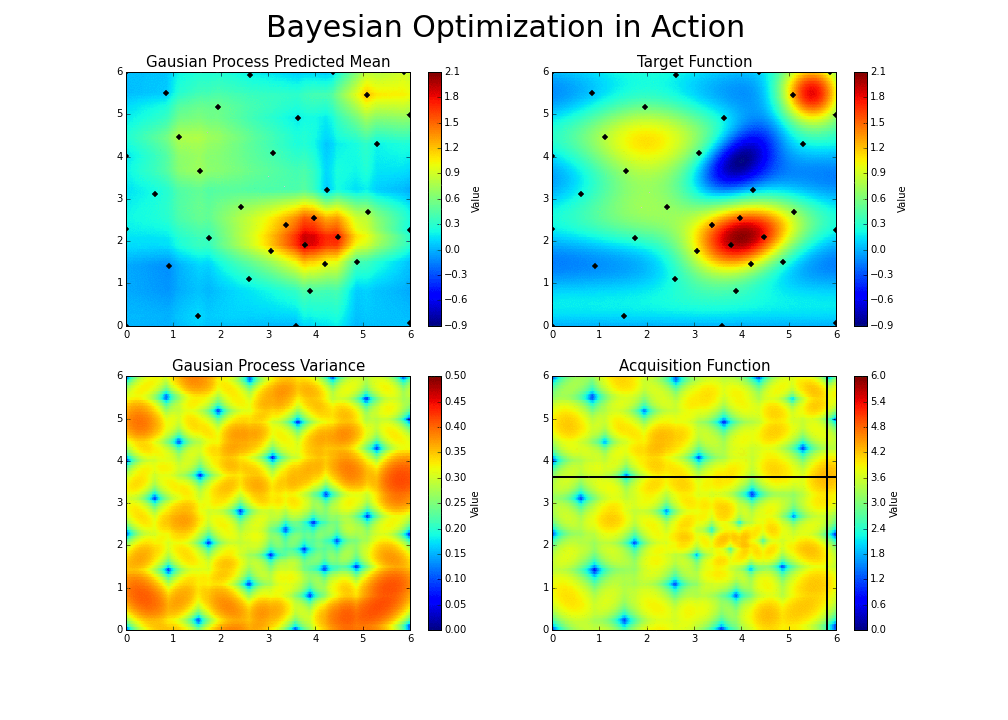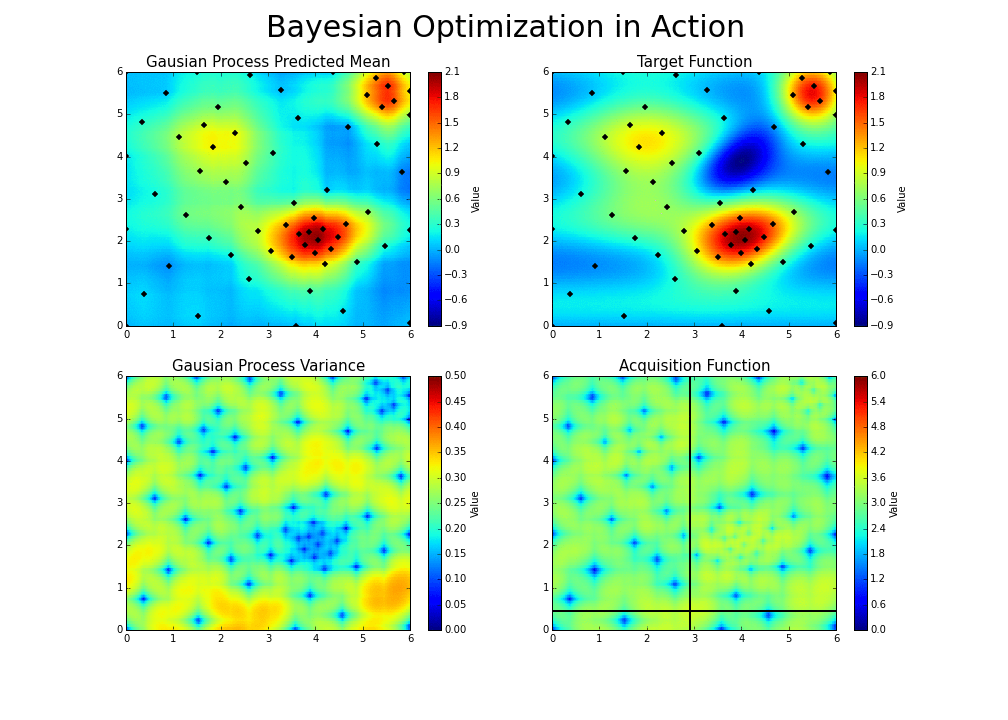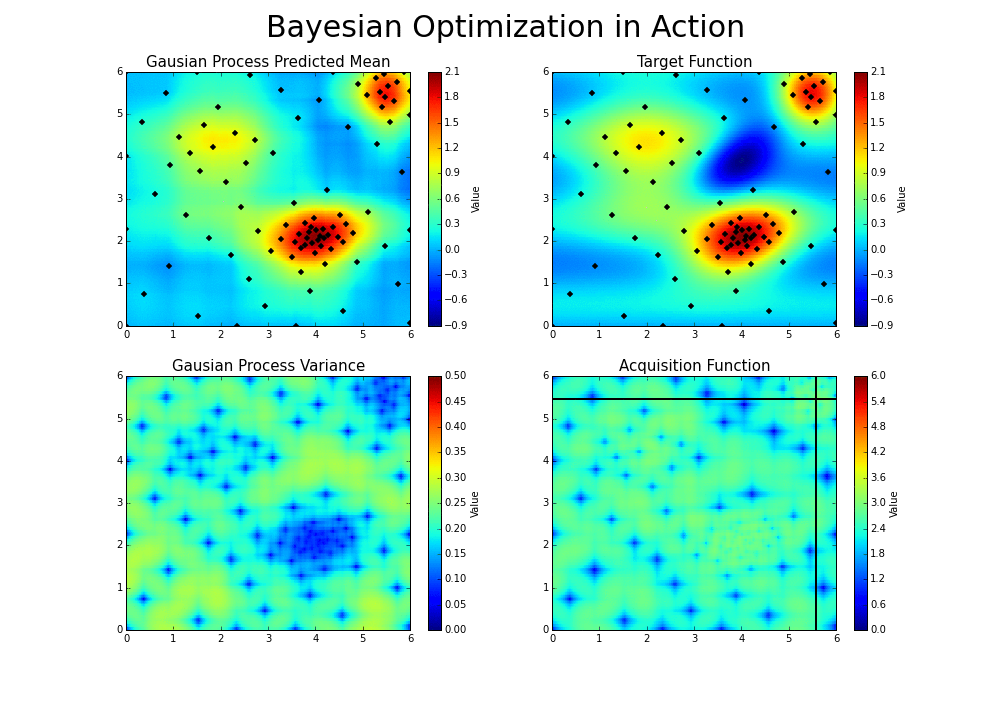
Implementation
Machine learning에서 optimization이 활용 될 수 있는 부분은 크게 다음 3가지이다:
- Algorithm Training. Optimization of model parameters. 주어진 훈련 데이터를 가지고 최적화.
- Algorithm Tuning. Optimization of model hyperparameters. 주어진 모델의 hyperparameter 최적화.
- Predictive Modeling. Optimization of data, data preparation, and algorithm selection.
Probability를 활용해서 위 optimization 과정을 수행할 수 있는 기법이 Bayesian optimization이다. The Bayesian Optimization algorithm can be summarized as follows:
- Select a Sample by Optimizing the Acquisition Function.
- Evaluate the Sample With the Objective Function.
- Update the Data and, in turn, the Surrogate Function.
- Go To 1.
주요 terms:
Samples: Samples are drawn from the domain and evaluated by the objective function to give a score or cost. One example from the domain, represented as a vector.
Search Space: Extent of the domain from which samples can be drawn.
Objective Function: Function that takes a sample and returns a cost.
Cost: Numeric score for a sample calculated via the objective function.
Surrogate Function: Bayesian approximation of the objective function that can be sampled efficiently. is used to best approximate the mapping of input examples to an output score. Probabilistically, it summarizes the conditional probability of an objective function (f), given the available data (D) or *P(f D)*. Acquisition Function: Technique by which the posterior is used to select the next sample from the search space.
There are many different types of probabilistic acquisition functions that can be used, each providing a different trade-off for how exploitative (greedy) and explorative they are.
Three common examples include:
- Probability of Improvement (PI).
- Expected Improvement (EI).
- Lower Confidence Bound (LCB).
byes_opt의 BayesianOptimization을 활용한 unknown function optimization 예시)
from bayes_opt import BayesianOptimization
def black_box_function(x, y):
"""Function with unknown internals we wish to maximize.
This is just serving as an example, for all intents and
purposes think of the internals of this function,
i.e.: the process which generates its output values, as unknown."""
return -x ** 2 - (y - 1) ** 2 + 1
# Bounded region of parameter space
pbounds = {'x': (2, 4), 'y': (-3, 3)}
optimizer = BayesianOptimization(
f=black_box_function,
pbounds=pbounds,
random_state=1,
)
optimizer.maximize(
init_points=2,
n_iter=3,
)
print("max: ", optimizer.max)
for i, res in enumerate(optimizer.res):
print("Iteration {}: \n\t{}".format(i, res))
max: {'target': -4.441293113411222, 'params': {'y': -0.005822117636089974, 'x': 2.104665051994087}}
>>> Iteration 0:
>>> {'target': -7.135455292718879, 'params': {'y': 1.3219469606529488, 'x': 2.8340440094051482}}
>>> Iteration 1:
>>> {'target': -7.779531005607566, 'params': {'y': -1.1860045642089614, 'x': 2.0002287496346898}}
>>> Iteration 2:
>>> {'target': -19.0, 'params': {'y': 3.0, 'x': 4.0}}
>>> Iteration 3:
>>> {'target': -16.29839645063864, 'params': {'y': -2.412527795983739, 'x': 2.3776144540856503}}
>>> Iteration 4:
>>> {'target': -4.441293113411222, 'params': {'y': -0.005822117636089974, 'x': 2.104665051994087}}
optimization 과정동안에 parameter bounds를 변경하고 싶으면, set_bounds method를 활용할 수 있다. You can pass any combination of existing parameters and their associated new bounds.
optimizer.set_bounds(new_bounds={"x": (-2, 3)})
optimizer.maximize(
init_points=0,
n_iter=5,
)
또한, domain reduction을 통해 initial bounds가 너무 넓은 경우, current optimal value를 중심으로 domain을 줄여볼 수 있다. 이를 통해 search progress 속도를 높일 수 있다. Using the SequentialDomainReductionTransformer the bounds of the problem can be panned and zoomed dynamically in an attempt to improve convergence. An example of using the SequentialDomainReductionTransformer is shown in the domain reduction notebook.
만약 대략적인 optimal point에 대한 idea가 있다면, probe를 통해 optimization을 guide할 수 있다.
optimizer.probe(
params={"x": 0.5, "y": 0.7},
lazy=True,
)
optimizer.probe(
params=[-0.3, 0.1],
lazy=True,
)
# Will probe only the two points specified above
optimizer.maximize(init_points=0, n_iter=0)
| iter | target | x | y |
-------------------------------------------------
| 11 | 0.66 | 0.5 | 0.7 |
| 12 | 0.1 | -0.3 | 0.1 |
=================================================
Optimization의 결과를 save, load, restart할 수도 있다.
By default the previous data in the json file is removed. If you want to keep working with the same logger, the reset paremeter in JSONLogger should be set to False.
from bayes_opt.logger import JSONLogger
from bayes_opt.event import Events
logger = JSONLogger(path="./logs.json")
optimizer.subscribe(Events.OPTIMIZATION_STEP, logger)
# Results will be saved in ./logs.json
optimizer.maximize(
init_points=2,
n_iter=3,
)
Optimization progress를 save했다면, 새로운 BayesianOptimization instance에 load할 수 있다. util submodule에서 load_log함수를 불러와서 save했던것을 다음과 같이 다시 시작할 수 있다.
from bayes_opt.util import load_logs
new_optimizer = BayesianOptimization(
f=black_box_function,
pbounds={"x": (-2, 2), "y": (-2, 2)},
verbose=2,
random_state=7,
)
# New optimizer is loaded with previously seen points
load_logs(new_optimizer, logs=["./logs.json"]);
Scikit-learn의 GaussianProcessRegressor를 활용한 Bayesian optimization 예시)
# example of bayesian optimization for a 1d function from scratch
from math import sin
from math import pi
from numpy import arange
from numpy import vstack
from numpy import argmax
from numpy import asarray
from numpy.random import normal
from numpy.random import random
from scipy.stats import norm
from sklearn.gaussian_process import GaussianProcessRegressor
from warnings import catch_warnings
from warnings import simplefilter
from matplotlib import pyplot
# objective function
def objective(x, noise=0.1):
noise = normal(loc=0, scale=noise)
return (x**2 * sin(5 * pi * x)**6.0) + noise
# surrogate or approximation for the objective function
def surrogate(model, X):
# catch any warning generated when making a prediction
with catch_warnings():
# ignore generated warnings
simplefilter("ignore")
return model.predict(X, return_std=True)
# probability of improvement acquisition function
def acquisition(X, Xsamples, model):
# calculate the best surrogate score found so far
yhat, _ = surrogate(model, X)
best = max(yhat)
# calculate mean and stdev via surrogate function
mu, std = surrogate(model, Xsamples)
mu = mu[:, 0]
# calculate the probability of improvement
probs = norm.cdf((mu - best) / (std+1E-9))
return probs
# optimize the acquisition function
def opt_acquisition(X, y, model):
# random search, generate random samples
Xsamples = random(100)
Xsamples = Xsamples.reshape(len(Xsamples), 1)
# calculate the acquisition function for each sample
scores = acquisition(X, Xsamples, model)
# locate the index of the largest scores
ix = argmax(scores)
return Xsamples[ix, 0]
# plot real observations vs surrogate function
def plot(X, y, model):
# scatter plot of inputs and real objective function
pyplot.scatter(X, y)
# line plot of surrogate function across domain
Xsamples = asarray(arange(0, 1, 0.001))
Xsamples = Xsamples.reshape(len(Xsamples), 1)
ysamples, _ = surrogate(model, Xsamples)
pyplot.plot(Xsamples, ysamples)
# show the plot
pyplot.show()
# sample the domain sparsely with noise
X = random(100)
y = asarray([objective(x) for x in X])
# reshape into rows and cols
X = X.reshape(len(X), 1)
y = y.reshape(len(y), 1)
# define the model
model = GaussianProcessRegressor()
# fit the model
model.fit(X, y)
# plot before hand
plot(X, y, model)
# perform the optimization process
for i in range(100):
# select the next point to sample
x = opt_acquisition(X, y, model)
# sample the point
actual = objective(x)
# summarize the finding
est, _ = surrogate(model, [[x]])
print('>x=%.3f, f()=%3f, actual=%.3f' % (x, est, actual))
# add the data to the dataset
X = vstack((X, [[x]]))
y = vstack((y, [[actual]]))
# update the model
model.fit(X, y)
# plot all samples and the final surrogate function
plot(X, y, model)
# best result
ix = argmax(y)
print('Best Result: x=%.3f, y=%.3f' % (X[ix], y[ix]))
Bayesian optimization을 통한 hyperparameter tuning 예시)
# example of bayesian optimization with scikit-optimize
from numpy import mean
from sklearn.datasets import make_blobs
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from skopt.space import Integer
from skopt.utils import use_named_args
from skopt import gp_minimize
# generate 2d classification dataset
X, y = make_blobs(n_samples=500, centers=3, n_features=2)
# define the model
model = KNeighborsClassifier()
# define the space of hyperparameters to search
search_space = [Integer(1, 5, name='n_neighbors'), Integer(1, 2, name='p')]
# define the function used to evaluate a given configuration
@use_named_args(search_space)
def evaluate_model(**params):
# something
model.set_params(**params)
# calculate 5-fold cross validation
result = cross_val_score(model, X, y, cv=5, n_jobs=-1, scoring='accuracy')
# calculate the mean of the scores
estimate = mean(result)
return 1.0 - estimate
# perform optimization
result = gp_minimize(evaluate_model, search_space)
# summarizing finding:
print('Best Accuracy: %.3f' % (1.0 - result.fun))
print('Best Parameters: n_neighbors=%d, p=%d' % (result.x[0], result.x[1]))
Best Accuracy: 0.976
Best Parameters: n_neighbors=3, p=2
References
- The Beauty of Bayesian Optimization, Explained in Simple Terms : https://towardsdatascience.com/the-beauty-of-bayesian-optimization-explained-in-simple-terms-81f3ee13b10f
- How to Implement Bayesian Optimization form Scratch in Python : https://machinelearningmastery.com/what-is-bayesian-optimization/
- https://github.com/fmfn/BayesianOptimization