DNN 훈련 효율/성능을 높이는 방법
연결가중치에 좋은 초기화 전략 적용
좋은 활성화 함수 사용
batch normalization 사용
보조작업 또는 비지도 학습을 통해 사전훈련된 network의 일부 재사용 (skipped less relevant to parameters)
고속 optimizer사용
희소 모델 사용
학습률 scheduling
규제
연결가중치 초기화 설정
gradient 손실
출력층에서 입력층으로 오차 gradients를 전파하면서 역전파 algorithm을 진행한다. 신경망의 모든 parameter에 대한 오차 함수의 gradient를 계산하면 SGD단계에서 이 gradient를 사용하여 각 parameter를 수정한다. 이때에 algorithm이 하위층으로 진행할 수 록 gradient가 점점 작아지는 경우가 발생할 수 있다. SGD를 통해 연결 가중치를 변경하지 않은채로 두게되어 결국 훈련이 좋은 솔루션으로 수렴되지 않는다.
gradient 폭주
gradient 손실과는 반대로 gradient가 너무 커져서 비이상적으로 큰 가중치로 갱신되고 역전파 algorithm이 진행되다가 발산(diverse/explode)해 버리는 경우가 발생할 수 있다. Gradient 폭주는 주로 순환신경망에서 많이 발생한다. gradient 폭주의 경우, 불안정한 gradient로 인해 층마다 학습 속도가 매우 달라져서 심층 신경망의 훈련이 어려워 진다.
적절한 gradient 역전파
활성화 함수를 잘 선택해야 gradient 손실이나 폭주를 방지할 수 있다.
적절한 gradient 역전파 algorithm 진행을 위해 다음 2 가지가 지켜져야한다:
- gradient를 역전파 할때에는 영방향으로 양방향 신호가 적절한 수준으로 전달되어야한다. (신호의 폭주/소멸을 방지해야함.) 적절한 수준을 유지하기 위해서는 각 층의 출력에 대한 분산이 입력의 분산과 동일해야한다.
- 역방향에서 층이 통과하기 전과 후의 gradient 분산이 동일해야한다.
fan_in: 입력의 연결 개수
fan_out: 출력의 연결 개수
fan_in과 fan_out이 같지 않다면, 위 두가지 사항이 지켜지기 어렵다.
fan_avg = (fan_in + fan_out)/2
이런 현상을 도입하기 위해, 각 층의 연결 가중치를 다음 공식대로 무작위로 초기화한다. 이를 Xavier initialization 또는 Glorot initialization이라고 부른다.
활성화 함수마다 적절한 초기화 전략이 있다.
| 초기화 전략 | 활성화 함수 | 정규분포(sigma^2) |
|---|---|---|
| Glorot | 활성화 함수 없음/ tanh/ logistic/ softmax | 1/fan_avg |
| He | ReLU(ELU를 포함한 ReLU의 변종들) | 2/fan_in |
| LeCun | SELU | 1/fan_in |
활성화 함수
적절한 활성화 함수를 선택해서 실행 속도 향상, 과대적합 억제, 등 network의 훈련과정과 성능을 개선할 수 있는 여러가지 효과를 만들어 낼 수 있다.
일반적으로 주로 선호하는 활성화 함수 순서대로 나열해보면:
SELU > ELU > LeakyReLU(그리고 변종들) > ReLU > tanh > logistics
ReLU
ReLU는 continuous한 함수이지만, z=0에서 미분가능하지 않다. (기울기가 갑자기 높아져서 경사 하강법이 어뚱한 곳으로 튈 수 있음) 그리고 z<0일 경우에도 함수는 0이지만, 실제로 잘 작동하고, 계산 속도가 빨라서 기본적인 활성화 함수로 많이 사용됨. 가장 큰 장점으로 출력에 최대값이 없다는 점이 경사 하강법에 있는 문제를 일부 완화해줌.
LeakyReLU
ReLu함수를 주로 사용하지만, “죽은 ReLU(dying ReLU)”로 알려진 문제가 있다. 훈련하는 동안 일부 뉴런이 0 이외의 값을 출력하지 않는다는 의미임. 특히 큰 학습률을 사용하면, 신경망의 뉴런 절반이 죽어있기도 함. (모든 샘플에 대해 입력의 가중치 합이 음수가되면, 뉴런이 죽게된다. 가중치 합이 음수이면 ReLU함수의 gradient가 0이 되기때문에 SGD가 더 작동하지 않음.)
이런 경우 문제해결을 위해 LeakyReLU와 같은 ReLU의 변종을 사용한다.
Hyperparameter alpha가 이 함수가 ‘새는(leaky)’ 정도를 결정한다. (새는 정도: z<0일때에 이 함수의 기울기이며, 일반적으로 0.01로 설정함. 이 작은 기울기때문에 LeakyReLU가 절대 죽지않는다. 즉 혼수상태로 떨어지지만, 죽지는않고 다시 깨어날 가능성을 유지하는 것이다.) 다음 graph와 같이 음수부분이 작은 기울기를 가지게되어 0이 되지는 않는다.
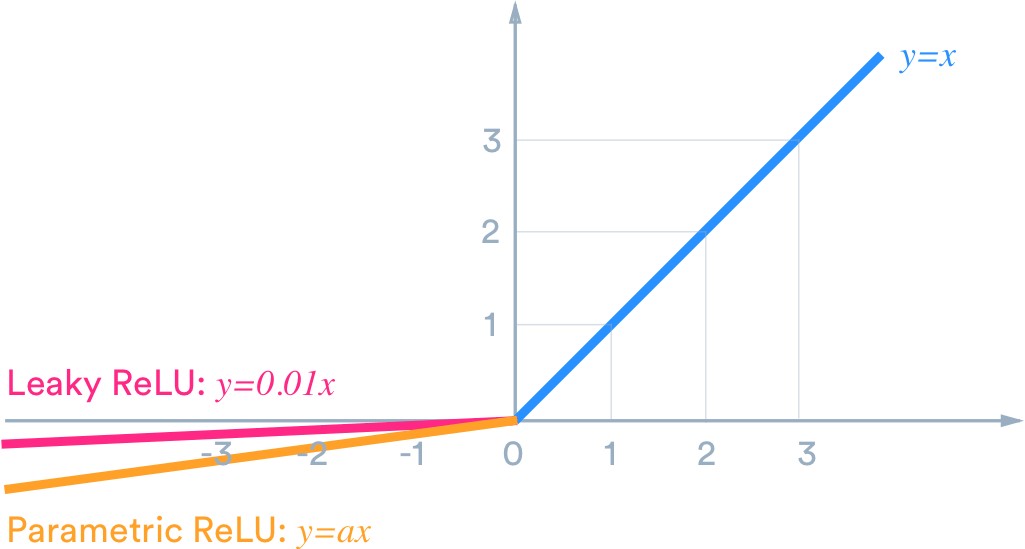
LeakyReLU의 종류로는 RReLU(Randomized leaky ReLU)와 PReLU(parametric leaky ReLU)가 있다.
RReLU(Randomized leaky ReLU) - 훈련하는 동안 주어진 범위에서 alpha를 무작위로 선택하고 테스트한다.
PReLU(parametric leaky ReLU) - alpha가 hyperparameter가 아니고 다른 model parameter들 처럼 역전파에 의해 변경된다. 소규모 데이터 input에서는 훈련세트에 과대적합 될 위험이 있다.
ELU (Exponential linear unit) -
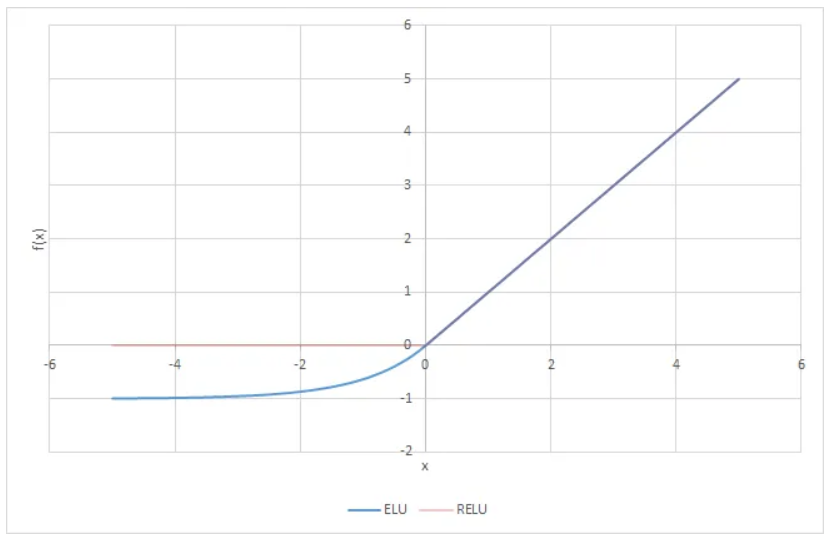
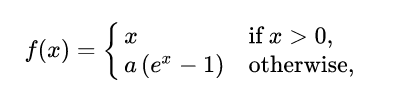
ELU의 장점:
- gradient 손실 문제 방지: z<0일 때에 (음수값이 들어오기때문에) 활성화 함수의 평균 출력이 0에 더 가까워짐. gradient가 0이 되지 않기때문에 neuron이 죽지는 않고, hyperparameter alpha를 통해 ELU가 수렴할 값을 정의할 수 있다. (보통 alpha를 1로 설정하지만, 양수의 다른 값으로 설정할 수 있음.)
- alpha=1이면, z=0에서 급격하게 변동하지 않기때문에 z=0을 포함해서 모든 구간에서 매끄러워 경사 하강법의 속도를 높여준다.
단점:
- 지수함수를 사용하기때문에 속도가 느린편이다. (ReLU나 그 변종들보다 계산이 느림.) 훈련하는 동안에는 수렴 속도가 빨라서 느린 계산이 상쇄되지만, test시에는 ELU를 사용한 network가 ReLU를 사용한 network보다 느리다.
SELU(scaled ELU):
SELU를 뉴런의 활성화 함수로 사용하면, 훈련하는 동안 각 층의 풀력이 평균0과 표준편차 1을 유지한다. 그래서 gradient의 손실과 폭주가 방지된다. 다음과 같은 사항들이 만족되면 network가 자기 정규화 (self-normalize)된다.
- input feature들이 표준화(mean=0, standard deviation=1)되어야한다.
- 모든 은닉층이 가중치가 lecun_normal로 초기화되어야함. (kernel_initializer=”lecun_normal”로 설정)
- network는 일렬로 쌓은 층으로 구성되어야한다. 순환 신경망이나 skip connection과 같이 순차적이지 않은 구조에서는 SELU로 self-normalize하는 것이 보장되지 못한다.
perceptron의 activation 함수로 다음과 같이 다양한 option을 활용해서 알고리즘이 원하는 방향으로 작동할 수 있도록 유도할 수 있다.
Logistics:
그림 1의 TLU에서 계단 함수는 수평선으로 되어있어서 gradient를 계산할 수 없기때문에 계단 함수를 logistic(sigmoid) 함수로 바꾼다. logistics 함수는 어디서든지 0이 아닌 continuous 값을 가지고있어서 gradient가 잘 정의될 수 있다.
tanh (hyperbolic tangent function):
logistic 함수처럼, 이 활성화함수 모양이 S이고, continuous해서 derivative를 찾을 수 있다. 출력 범위가 -1에서 1사이이고 훈련 초기에 각 층의 출력을 원점 근처로 모으는 경향이 있어서 model이 빠르게 수렴되도록 도와줌.
softmax:
출력 0에서 1사이 실수. softmax함수 출력의 총합은 1이다. 출력의 총 합이 1이 된다는것은 softmax의 매우 중요한 성질이다. 이 성질을 기반으로 softmax 함수의 출력을 “확률”로 해석할 수 있기때문이다.
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
언제 어떤 활성화 함수를 사용해야할까?
활성화 함수를 잘못 선택하면 gradient손실/ 폭주를 발생시킬 수 있다. 주의해야 함.
network가 self-normalize되지 못하는 구조 –> SELU보다 ELU(SELU가 z=0에서 연속적이지 않기때문)
실행 속도가 중요하다면 –> LeakyReLU(hyperparameter를 더 추가하고 싶지 않다면 케라스에서 사용하는 기본 alpha를 사용)
신경망이 과대적합 되어있다면 –> RReLU
훈련 세트가 매우 크다면 –> PReLU
보통 가장 널리 사용되는 활성화 함수이며, 많은 라이브러리와 hardware 가속기에 특화 되어있는 –> ReLU
참고: 다양한 activation 함수 소개: https://himanshuxd.medium.com/activation-functions-sigmoid-relu-leaky-relu-and-softmax-basics-for-neural-networks-and-deep-8d9c70eed91e
Batch normalization (배치 정규화)
gradient 손실과 폭주를 방지하기위해 개발한 기법임. ELU와 함께 He initialization을 사용하면 훈련 초기 단계에서 gradient 손실/폭주 문제를 억제할 수 있지만, 훈련하는동안 이런 문제가 아얘 발생하지 않는것이 보장되지는 못한다. 최근 Hongyi Zhang 등의 최근 논문에는 batch normalization 없이 가중치 초기화 기법만으로 심층 신경만을 훈련시켜서 매우 복잡한 이미지 분류 작업의 최고 성능을 확보했다(2019). 그러나 아직 이를 뒷받침할 추가 논문을 통해 타당성을 확인 해야함.
how-to:
각층에서 활성화 함수를 통과하기 전 or 후에 모델에 연산을 하나 추가한다:
- 단순하게 입력을 원점에 맞추고 정규화한 다음,
- 각 층에서 두 개의 새로운 parameter로 결과값의 스케일을 조정하고 이동시킨다. (하나는 scale 조정에, 다른 하나는 이동에 사용한다.)
만약 신경망의 첫번째 층으로 batch normalization을 추가하면, 훈련 세트를 표준화(e.g., via StandardScaler)할 필요가 없다. Batch normalization층이 표준화 역할을 대신한다.
입력을 원점에 맞추고 정규화하려면 - algorithm이 입력의 평균과 표준편차를 추정해야함. 이를 위해서 주어진 mini batch에서 입력의 평균과 표준편차를 평가한다. (batch의 normalization을 계산하기때문에 hence the name “batch normalization”)
훈련하는 동안에는 입력을 전규화 한다음, scale을 조정하고 이동시킨다. 반면, test시에는 샘플 하나에 대한 예측을 찾아야하기 때문에, 더 복잡하다. 입력에 대한 평균과 표준편차를 계산할 수 없기때문. IID 조건을 만족하지 못함.
keras에서는 batch normalization층 마다 입력 평균과 표준편차의 이동평균 (moving average)를 이용해서 훈련하는 동안 ‘‘최종’’ 통계를 추정한다. (‘최종’ 통계 - test시, 각 샘플의 대변하기위함. 전체 데이터 셋이 신경망을 통과해서 batch normlization층의 각 입력에 대한 평균과 표준편차를 계산하는 것과 같은 ‘최종’ 통계를 나타내도록 다음 4개의 paraemter vectors를 사용)
batch normalization층 마다 4 prameter vectors가 학습된다.
- 출력 scale vector - gamma
- 출력 이동 vector - beta
- 최종 입력 평균 vector - mu (“이동평균”)
- 최종 입력 표준편차 vector - sigma (“이동평균”)
여기에서 mu와 sigma는 훈련하는 동안 추정되지만, 훈련이 끝난 후에 사용됨.
활성화함수 이전/이후:
활성화 함수 이전에 batch normalization을 추가하려면 은닉층에서 활성화 함수를 지정하지말고 batch normalization 층 뒤에 별도의 층으로 추가해야함. batch normalization층 입력마다 이동 parameter를 포함하기 때문에 이전 층에서 편향을 뺄 수 있다. (층을 만들때, use_bias=False로 설정.)
BatchNormalization class에서 조정할 수 있는 hyperparameter:
momentum
적절한 값은 대부분 1에 가까움. (e.g., 0.9, 0.99, 0.999, 데이터셋이 크고 mini batch가 작으면, 1더 가깝게 증가시킨다.)
axis - 정규화할 축을 결정한다. 기본값은 -1
이동 평균 V_hat을 다음 공식을 사용해서 update한다.
장점:
- gradient손실, 폭주 문제 감소. tanh나 logistic 함수와 같이 수렴성을 가진 활성와 함수 사용 가능.
- 가중치 초기화에 network가 훨씬 덜 민감해짐
- 훨씬 큰 학습률을 사용하여 학습과정의 속도를 크게 높일 수 있음. (e.g., 이미지 분류 모델에 적용하면 정규화가 14배나 적은 훈련 단계에서도 같은 정확도를 달성한다.)
- 규제와 동일한 역할을 하기도 함.
단점:
- 모델의 복잡도를 키워서 실행시간 면에서 손해, 층마다 추가되는 계산이 신경망 예측을 느리게 한다. 그러나 batch normalization을 사용하면 수렴이 훨씬 빨라지기때문에 보통 상쇄됨. 오히려 더 적은 epoch로 동일한 성능을 확보할 수도 있음.
gradient clipping
gradient 폭주문제를 완화시키는 방식. 역전파가 진행될때 일정 임계값을 넘지못하게 gradient을 잘라내는것이다.
순환 신경망에서는 batch normalization을 적용하기 어려워서 gradient clipping 방식을 많이 사용한다.
model compile시, optimizer를 생성할때에 clipvalue와 clipnorm 매개변수를 지정하면 됨. clipvalue=1.0 지정 시, optimizer은 gradient vector의 모든 원소를 -1.0과 1.0사이로 clipping한다. 즉, 훈련되는 parameter에 대한 손실함수의 모든 편미분값을 -1.0에서 1.0안에 들어오도록 잘라내는것. 이 기능을 통해 gradient의 방향을 바꿀 수도 있다. 이런 문제를 방지하려면 clipnorm을 설정하면된다. clipnorm=1.0을 지정하면, gradient vector의 원소값들을 normalize해서 방향이 바뀌는 문제는 발생하지 않는다.
e.g. if gradient vector = [0.9, 100.0], then clipvalue=1.0 매개변수로 optimize가 정의되면, gradient vector = [0.9, 1.0]이 되어서 원래 두번째 축 방향을 향해야하는 것이 첫번째와 두번째의 대각선으로 바뀌여버린다. 만약 대신 clipnorm=1.0을 설정하면, gradient vector=[0.00899964, 0.9999595]로 방향이 유지된채 gradient값이 clipping될 수 있다.
고속 optimizer
여기에서 논의하는 최적화 기법은 1차 편미분(Jacobian)에만 의존한다. 최적화 이론에는 2차 편미분(Hessian)을 기반으로한 뛰어난 algorithm들이 많다. BUT! Hessian algorithm들은 심층 신경망에 적용하기 어렵다. 2차 편미분 알고리즘을 사용하게되면, n=parameter 개수일때, 하나의 출력마다 n개의 1차 편미분이 아니라 n^2개의 2차 편미분을 계산해야하기 때문이다. 심층 신경망은 보통 수만개의 parameter를 가지므로 2차 편미분 최적화 알고리즘은 memory 용량을 넘어서는 경우가 많다.
1차 편미분이 사용되는 SGD 대신 최적화를 위해 주로 사용되는 optimizer는 RMSProp과 Adam이다.
While SGD makes weight and bias updates independently, RMSprop makes its updates based upon the root mean square of the differentials of weights and biases, allowing a straighter trajectory towards the optimal loss value. The Adam optimizer works similar to RMSprop but includes a moving average of the second order moment of gradients for an adaptive learning rate.
RMSProp
RMSProp은 훈련 시작부터 모든 gradient가 아닌, 가장 최근 반복에서 비롯된 graidnet만 누적한다. 그래서 알고리즘의 첫번째 단계에세 지수 감소를 사용한다.
code 구현:
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
아주 간단한 문제를 제외하고는 RMSProp가 AdaGrad보다 성능이 더 좋다.
Adam
Adam = (적응적 모멘텀 최적화) Adaptive momtum optimizer (=momentum최적화 +RMSProp)
t는 (1부터 시작하는) 반복횟수를 의미한다.
beta_1는 momentum 감쇠 hyperparameter이고
beta_2는 scale감회 hyperparamter이다.
3,4번은 m과 s가 0으로 초기화되기때문에, 훈련 초기에 0으로 쏠리게되어있어서 이 둘의 값을 증폭시키는 역할을 한다.
1,2,5번은 RMSProp과 momentum 최적화 방식과 비슷함. 단, 1에서 지수 감소의 평균을 구한다.
code 구현:
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
Adam에서도 RMSProp과 AdaGrad에서 처럼 적응적 학습률/최적화 알고리즘이기때문에 학습률 hyperparameter (eta)를 튜닝할 필요가 적다.
momentum optimization(모맨텀 최적화)
경사하강법(SGD)에서는 이전 gradient가 얼마였는지 고려하지않는다.(그래서 gradient가 아주 작으면 매우 느려지는 문제 발생). Momentum optimization에서는 gradient가 얼마였는지는 매우 중요하게 고려한다.
모멘텀 알고리즘:
매 반복에서 현재 gradient를 학습률을 곱한 후, momentum vector m에 더하고 이 값을 빼는 방식으로 가중치를 갱신한다. 즉 gradient가 속도(velocity)가 아니라 가속도(acceleration)로 사용되는 것이다. (momentum의 차이 만큼 gradient가 변하기때문에, velocity의 차이만큼 acceleration이 변하는 것과 동등하다고 보면 된다?) 여기에서 Beta는 일종의 마찰저항을 표현하고 momentum이 너무 커지는것을 막아준다. Beta=(0,1) 일반적인 momentum값은 0.9이다.
terminal velocity (종단속도)를 구할때에 위 공식에서 1번의 좌우변을 equal하게 set해서 m을 구해보면 –> 종단속도는 학습률을 곱한 gradient에 (1/(1-beta))를 곱한것과 같은을 확인할 수 있다. beta가 0.9라면, (1/(1-beta))는 10이 되고, momentum 최적화가 SGD보다 10배는 더 빠르게 진행된다는것을 확인할 수 있다.
code 구현 방법:
compile시, SGD optimizer를 정의할때에 매개변수로 momentum을 전달하면된다.
optimizer = keras.optimizers.SGD(lr=0.001, momentun=0.9)
Nesterov accelerated gradient (NAG)
기본 momentum 방식에서 변종된 기법이다. 기본 momentum기법보다 더 빠르다. 현재 위치가 기존 gradient가 아니라 momentum 방향으로 조금 더 앞선 theta = theta + beta*m 에서 비용함수의 gradient를 계산한다.
NAG는 진동을 감소시키고 수렴을 빠르게 만들어준다.
code 구현 방법:
optimizer = keras.optimizers.SGD(lr=0.001, momentun=0.9, nesterov=True)
AdaGrad
기본 SGD는 가장 가파른 경사를 따라 빠르게 내려가기 시작한다. AdaGrad는 이와 다르게 좀 더 정확한 방향으로 이동한다. 가장 가파른 차원을 따라 gradient vector의 scale을 감소시켜서 전역 최적점 쪽으로 좀 더 정확한 방향을 잡는다. 단, AdaGrad가 너무 빨리 느려져서 최적점에 수렴하지 못하는 위험이 있다는 점을 주의해야한다.
NOTE: 여기에서 1의 multiply와 2의 divide는 각각 원소별 곱셈과 원소별 나눗셈을 의미한다.
첫번째 단계에서는 gradient의 제곱을 vector s에 누적한다. vector화된 식은 vector s의 각 원소 s_i는 parameter theta_i에 대한 비용함수의 편미분을 제곱하여 누적한다. (비용함수가 i번째 차원을 따라 가파르다면 s_i는 반복이 진행됨에 따라 점점 더 커질것임.)
두번째 단계에서는 기존 SGD와 비슷함. 한가지 파이는 gradient vector를 sqrt(s+e)로 나누어서 scale을 조정하는 것이다. (제곱을 했기때문에 sqrt(s)로 나누어서 scale 원복해야함. 여기에서 e는 0으로 나누게되는 것을 방지하기위해 작은 값이 더해진것이다.)
AdaGrad는 학습률을 감소시키지만 경사가 완만한 차원보다 가파른 차원에 대해 더 빠르게 감소된다. (이를 adaptive learning rate이라고 한다.) 전역 최적점 방향으로 더 곧장 가도록 갱신되는데에 도움이 된다. 그래서 AdaGrad에서는 학습률을 덜 tuning해도 된다.
AdaGrad는 신경망을 훈련할때에 너무 일찍 멈춰버리는 경향이 있다. 학습률이 너무 감소되어서 전역 최적점에 도착하기전에 알고리즘이 멈춰버린다. But linear regression과 같이 간단한 작업에는 효과적일 수 있다. keras에 포함된 optimizer이지만, 실제 심층 신경망을 훈련할때에는 사용하지 않는다.
Nadam
Nadam (= Adaptive momtum optimizer + Nesterov 기법)
Adam보다 조금 더 빠르게 수렴한다.
AdaMax
Adam은 시간에 따라 감쇠된 gradient의 L2 norm으로 parameter update scale을 낮춘다. Adamax는 L2 norm에서 L_inf norm으로 바꾸는 것이다. (L_inf는 vector max norm을 계산하는것과 같음.) theta를 갱신할때에 s에 비례하여 gradient update의 scale을 낮춘다. 시간에 따라 감쇠된 gradient의 최대값이다. 실전에서는 AdaMax가 Adam보다 더 안정적이다. 데이터셋에따라 다르기때문에 Adam이 잘 동작하지 않는다면, AdaMax를 시도해볼 수 있다.
회소 모델 훈련 (sparse model trianing)
모든 최적화 알고리즘은 대부분의 parameter가 0이 아닌 dense 모델을 만든다. 만약 엄청 빠르게 실행할 모델이 필요하거나 메모리를 적게 차지하는 모델이 필요하면 dense(밀집) model이 아닌, sparse(희소) model을 만들어서 훈련을 진행할 수 있다.
학습률 scheduling
한가지 전략은 - 큰 학습률로 시작하고 학습 속도가 느려질때 학습률을 낮추면 최적의 고정 학습률보다 좋은 솔루션을 더 빨리 발견할 수 있다. 훈련하는 동안 학습률을 어떻게 감소시킬지 - 감소시키는 전략에는 여러 방법이 있다. 이런 다양한 전략을 학습률 scheduling이라고 한다.
주로 사용되는 학습률 scheduling:
- 거듭제곱 기반 스케쥴링 (power scheduling)
- 지수기반 스케쥴링 (exponential scheduling)
- 구간별 고정 스케쥴링 (piecewise constant scheduling)
- 성능 기반 스케쥴링 (performance scheduling)
- 1 사이클 스케쥴링 (1cycle scheduling)
규제(regularization)
Regularization은 regression의 한 형태이다. regression equation의 coefficient를 constrain/regularize하거나 zero값으로 estimate하는 것이다.
“this technique discourages learning a more complex or flexible model, so as to avoid the risk of overfitting.”
dataset에서 feature들이 지나치게 많거나, training data에 noise가 많거나, training대비 testing 성능이 부족한경우, model의 generalization 부족하여 overfitting 이슈가 발생할 수 있다. 즉, 주어진 input에만 상세하게 맞춰진 model이 생성되어서 새로운 data가 주어졌을때에 정확도가 떨어지는 prediction output을 만들어내는 것이다.
이를 방지하기위해 모델의 학습 과정동안 cost/loss function의 최소값을 위한 parameter를 계산할때에 규제(regularization)을 활용할 수 있다.
예측하려는 샘플의 분류가능한 class가 2개 이상일때에 다중 분류 모델을 활용한다. 주로 C매개변수 & max_iter가 사용된다.
반복적인 알고리즘을 사용하기 때문에 max_iter 매개변수의 값을 어느정도 큰 값으로 설정한다. (참고: 기본값 100에서 1,000으로 늘려야 경고가 발생하지 않는다.)
LogisticRegressioin은 기본적으로 릿지 회귀와 같이 계수의 제곱을 규제한다.(L2)
- 릿지에서 alpha매개변수로 규제의 양을 조절했지만 LogisticRegression에서는 C매개변수를 사용한다.
- C매개변수는 커지면 완화된다. 기본값이 1이지만, 완화하기위해 20으로 지정한다. (C 매개변수는 ridge의 alpha와는 반대 경향)
Ridge (L2)
loss function에 더할 shrinkage quantity를 정의해서 penality의 크기를 정한다. 즉, coefficient를 얼만큰 규제할 지를 정의하는 것이다. ridge regression은 constrain하려는 coefficient를 완전하게 zero로 만들지는 못하지만, zero에 가깝게 constrain할 수 있다.
L2 regularization. 기존 cost function에 다음과 같이 penalty를 더한다.
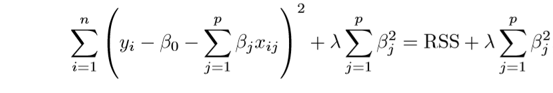
ridge는 parameter (i.e. weights)에 규제를 더한다. penalty term lambda를 통해서 regression의 coefficient를 감소시킨다. 이는 model complexity와 multicollinearity를 감소시켜준다.
“λ is the tuning parameter that decides how much we want to penalize the flexibility of our model”
when λ → 0 , the cost function becomes similar to the linear regression cost function (eq. 1.2). So lower the constraint (low λ) on the features, the model will resemble linear regression model.
Ridge는 coefficients를 zero에 가깝게는 감소시키지만, 완전히 zero로 만들어서 제외하지는 못한다.
반대로, as λ→∞, the impact of the shrinkage penalty grows, and the ridge regression coefficient estimates will approach zero.
적절한 λ를 찾는것이 매우 critical하다. cross validation을 통해 최적을 λ를 찾을 수 있다. The coefficient estimates produced by this method are also known as the L2 norm.
한가지 주의할 점은 - ridge regression을 수행하기 전에 predictor를 standardize하거나 predictor를 ridge regression과 동일한 scale로 변한시켜놓아야 한다.
Lasso (L1)
L1 regularization. Least absolute shrinkage와 selection operator를 통해서 다음과 같이 penalty를 더한다. Lasso는 제외하고싶은 coefficient는 완전하게 제외할 수 있는 강점이 있다.
| “This variation differs from ridge regression only in penalizing the high coefficients. It uses | βj | (modulus)instead of squares of β, as its penalty. In statistics, this is known as the L1 norm.” |
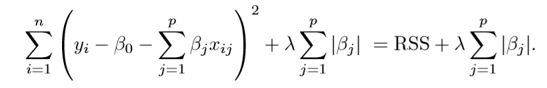
ridge와 비슷하지만 penalty로 가져가는 값이 squared가 아닌 magnitude라는 점이 다르다. Lasso와 같은 방식으로 규제를 하게되면 zero coefficient를 갖게될 수도 있다. 즉, 특정 feature이 output evaluation에서 완전히 제외되도록 설정할 수 있는것이다. Lasso는 overfitting을 방지하는 목적외에도 feature selection에도 활용될 수 있는 technique이다. (official documentation: https://scikit-learn.org/stable/modules/linear_model.html#lasso)
feature를 selectively 사용할 수 있게 해주는것을 compressive sensing이라고도 부름.
ridge & lasso in different perspective:
“The ridge regression can be thought of as solving an equation, where summation of squares of coefficients is less than or equal to s. And the Lasso can be thought of as an equation where summation of modulus of coefficients is less than or equal to s.(Here, s is a constant that exists for each value of shrinkage factor λ. These equations are also referred to as constraint functions.)”
regularization을 constraint function으로 생각하며 다음 exmaple들에 regularization이 어떤 영향을 주는지 확인해볼 수 있다.
2개의 parameter가 주어진 problem에서,
ridge regression은:
β1² + β2² ≤ s
이 equation은 geometrically a circle를 의미한다. therefore implies that ridge regression coefficients have the smallest RSS(loss function) for all points that lie within the circle given by β1² + β2² ≤ s.
lasso는:
| β1 | + | β2 | ≤ s |
| 이 equation은 geometrically a diamond를 의미한다. therefore implies that lasso coefficients have the smallest RSS(loss function) for all points that lie within the diamond given by | β1 | + | β2 | ≤ s. |
다음 그림에서 red ellipse contour는 RSS를 의미하고, constraint functions (green areas)는 왼쪽은 lasso, 오른쪽은 ridge regression을 표현한다.
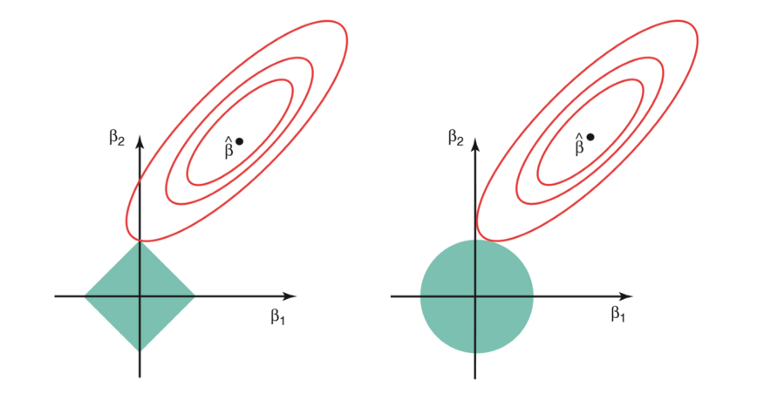
s 값이 커질수록 the green regions will contain the center of the ellipse (ridge/lasso techniques의 coefficient estimate가 least square estimates와 동일해짐.)
ridge regression이 circular constraints을 가지고 (no sharp points)있기때문에 intersection will not generally occur on an axis, so the ridge regression coefficientwill be exclusively non-zero.
ridge와는 다르게, lasso constraint는 each of the axes에 corner를 가지고있기때문에 ellipse will often intersect the constraint region at an axis. RSS(loss function) ellipse가 더 자주 constraint region at an axis와 intersect할 것 이다. 이렇게 intersect하는 경우, coefficient가 zero가 된다.
coefficient가 constrain되는 정도에서 ridge와 lasso사이에 차이점이 있다. ridge regression은 least important predictor의 coefficient를 zero에 가깝게 shrink 하지만, 완전하게 zero로 만들지는 못한다. In other words, the final model will include all predictors.
그러나 lasso의 경우, 제외하고 싶은 least important predictor의 coefficient를 완전하게 zero값으로 만들어버릴 수 있다. the L1 penalty has the effect of forcing some of the coefficient estimates to be exactly equal to zero when the tuning parameter λ is sufficiently large. Therefore, the lasso method also performs variable selection and is said to yield sparse models.
이 차이점은 model interpretability에서 ridge regression의 disadvantage이다.
dropout
dropout 비율 p를 설정해서 매 훈련 step에서 각 neuron이 임시적으로 dropout될 활률을 의미한다. (즉, 이번 step에서는 와전히 무시되지만, 다음 스텝에서는 활성화될 수 있다.) 보통 10~50%사이 값을 지정한다. 순환 신경망에서는 20~30%, 합곱신경망에서는 40~50%사이 값을 지정.
MonteCarlo dropout(MC dropout)
monte class에서 설정하는 dropout
dropout층 상속, call method override하고, training 매개변수를 True로 설정
max-norm regularization
불안정한 gradient를 완화하는데에 활용한다. 매개변수 bias constraints를 조정하여 편향을 조정한다.
실용적 guideline
모든 case에 맞는 명확한 기준은 없지만, hyperparameter tuning을 크게 하지 않고 대부분의 경우에 잘 맞는 조건은 다음과 같다:
기본 DNN설정:
| hyperparameter | default |
|---|---|
| 커널 초기화 | He 초기화 |
| 활성화 함수 | ELU |
| 정규화 | 얕은 신경망일 경우 없음 \ 깊은 신경망일 경우 배치정규화 |
| 규제 | 조기 종료(필요시 L2 규제 추가) |
| 옵티마이져 | momentum 최적화 (또는 RMSProp or Nadam) |
| 학습률 스케쥴 | 1 cycle |
만약 network가 완전 연결층을 쌓은 단순한 모델이라면, 다음과 같이 자기 정규화를 사용할 수 있다.
자기 정규화를 위한 설정:
| hyperparameter | default |
|---|---|
| 커널 초기화 | LeCun 초기화 |
| 활성화 함수 | SELU |
| 정규화 | 없음(자기 정규화) |
| 규제 | 필요시 alpha dropout |
| 옵티마이져 | momentum 최적화 (또는 RMSProp or Nadam) |
| 학습률 스케쥴 | 1 cycle |
pytorch - compile 및 fit 방식 확인 필요 (build, etc)
Reference
- Geron, Aurelien. Hands on Machine Learning. O’Reilly, 2019
- https://towardsdatascience.com/regularization-in-machine-learning-76441ddcf99a