RNN (recurrent neural network)

times series data(data가 sequence 형태이거나 data내의 순서가 의미가 있을때)를 학습해서 예측값을 찾으려 할때에는 RNN(순환 신경망)을 사용한다. RNN은 고정된 길이의 입력이 아닌 임이의 길이를 가진 sequence를 다룰 수 있다. (e.g., 문장, 문서, 오디오 샘플, 등) 기본적으로 RNN이 사용될 수 있지만, 제한적인 단기 기억을 다루도록 기능을 향상하기 위해서는 LSTM과 GRU cell을 사용해서 모델을 확장할 수 있다.

RNN기본 개념

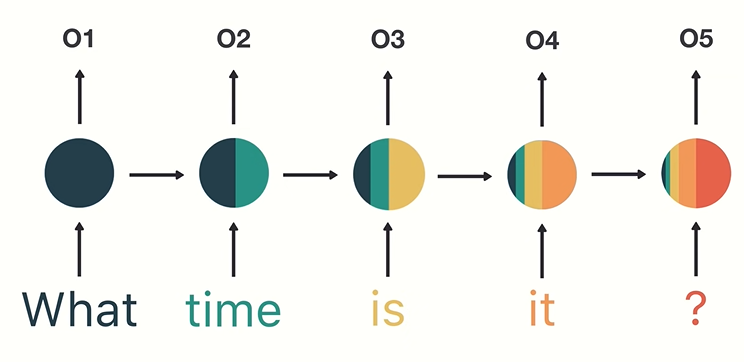
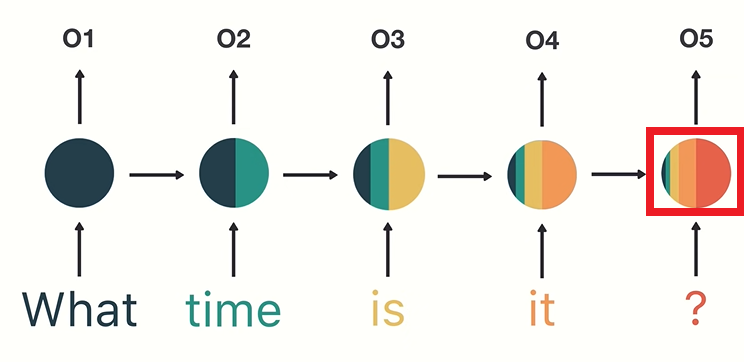
what, time, is, it, ? 으로 구성된 메세지가 input으로 주어진다면 RNN이 이 input을 학습하는 과정을 간단하게 illustrate하자면 다음과 같다:

전체적인 control flow written in code:

input의 word 순서대로 recursive하게 rnn함수가 호출되어 output과 hidden이 생성되고, 마지막 output을 사용하여 prediction을 생성한다.

RNN은 feedforward 신경망과 비슷하지만, 각 neuron을 보면 뒤쪽으로 순환하는 연결이 있다는 점이 다르다. 다음 그림과 같이 neuron A는 입력 x를 받아서 출력 h를 만드는것 외에도 자신에게 보내는 출력을 만든다.

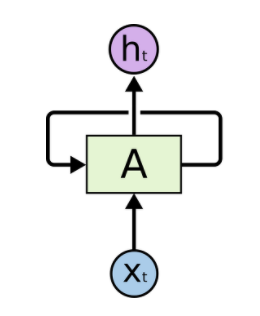
time step t에서 순환 neuron의 출력은 이전 time step의 모든 입력에 대한 함수이기때문에 일종의 메모리 형태라고 할 수 있다. time step에 걸쳐서 어떤 상태를 보존하는 신경망의 구성 요소를 memory cell이라고 한다. 조금 더 상세하게 들여다보면 다음 그림과 같이 표현할 수 있다.

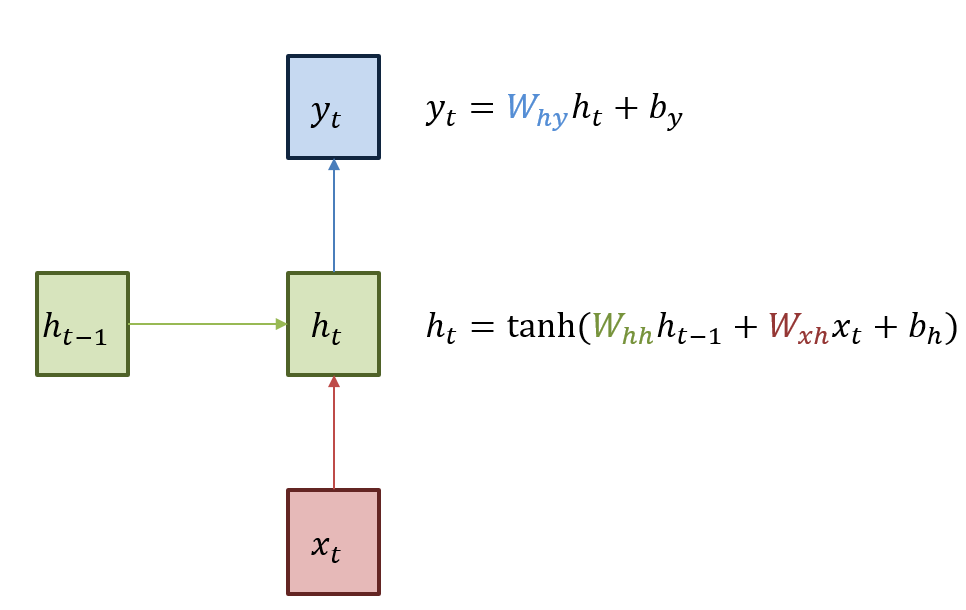
여기에서 cell의 상태를 h로 나타내는데, hidden 은닉을 의미한다. hidden이 사용되는 이유는 현 state에서 이전 time step에서 온 정보가 “은닉”되어 있다고 여겨지기 때문이다.

time step t에서의 cell 상태를 h_t로 표현하는데, 이는 그 time step의 입력과 이전 time step의 상태에 대한 함수이다. 순환 neuron은 각 time step(또는 frame) t 마다 x_t와 이전 time step의 출력인 h_ (t-1)를 입력으로 받는다.

recurrent network에서는 활성화 함수로는 ReLU대신 tanh를 많이 사용한다. 각 순환 neuron은 두개의 가중치를 가진다. 하나는 입력 x_t를 위한것이고 다른 하나는 이전 time step의 출력 h_ (t-1)를 위한 것이다. 이 가중치를 w_xh, w_hh로, 편향을 b_h로 표현해서 다음과 같이 recurrent neuron의 출력을 표현할 수 있다.

# 코드로 표현한 neuron하나로 구성된 하나의 층을 가진 간단한 RNN
model = keras.models.Sequential([
    keras.layers.SimpleRNN(1, input_shape=[None,1])
])

RNN은 입력 sequence를 받아서 출력 sequence를 만들 수 있다. 예를 들어서 sequence-to-sequence network는 주식가격같은 시계열 데이터를 예측하는데에 유용하다. (최근 N일치의 주식 가격을 주입하면 network는 각 입력값보다 하루 앞선 가격을(N-1일 전부터 내일까지) 출력한다.

sequence-to-vector network은 입력 시퀀스를 network에 주입하고, 마지막을 제외한 모든 출력을 무시할수도 있다. 예를 들어서 영화 리뷰에 있는 연속된 단어를 주입하면 network는 감성점수를 출력한다.

반대로 각 time step에서 하나의 입력 vector을 반복적으로 network에 입력하고, 하나의 sequence를 출력하는 vector-to-sequence network도 존재한다. 예를 들어 이미지(또는 CNN의 출력)을 입력하여 이미지에 대한 caption을 출력할 수 있다.

encoder라고 불리는 sequence-to-vector network뒤에 decoder라고 불리는 vector-to-sequence network을 연결하면 “encoder-decoder”라고 부르는 구조가 만들어지고 예를 들어서 한 언어의 문장을 다른 언어로 번역하는데에 활용될 수 있다. 한 언어의 문장을 network에 입력하면, encoder는 이 문장을 하나의 vector로 표현하고, 이 vector는 decoder를 통해 다른 언어의 문장으로 decoding된다. (이런 방식이 하나의 sequnce-to-sequence network을 사용해서 한단어씩 번역하는 것 보다 훨씬 더 잘 번역을 수행할 수 있다.)

RNN 훈련

RNN을 time step 순서대로 펼치고, 보통의 역전파를 사용해서 훈련을 진행할 수 있다. 이 방법은 BPTT(back propagation through time)이라고 불린다.

기존 역전파가 진행되는 것과 같이 먼저 정방향패스가 펼쳐진 network를 통과 하고 비용함수를 사용해서 출력 sequence를 평가한다. 그리고 비용함수의 gradient는 펼쳐진 network를 따라 역방향으로 전파된다. (이 비용함수는 일부 출력을 무시할 수 도있다. 예를 들어서 network의 마지막 출력 Y_n, Y_ (n-1), Y_ (n-2) 만 사용해서 비용함수를 계산하고 gradient는 이 세 개의 출력을 거치고 Y_0, Y_1, …등의 앞의 출력들은 거치지 않는다.) model parameter들은 BPTT동안 계산된 gradient를 사용해서 update된다. 각 time step마다 같은 매개변수 W와 b가 사용되기때문에 역전파가 진행되면 모든 time step에 결쳐 합산된다.

RNN의 backpropagation이 진행되면서 time step의 gradient를 계산할때에 이전 step의 gradient를 기반으로 계산되기때문에 vanishing gradient 문제가 발생할 위험이 크다. 즉, input sequence의 앞쪽의 정보일수록 “오래된 기억”이기때문에 제대로 고려되지 못하는 문제가 발생하는 것이다. “What time is it?”이 주어졌을때, “What”과 “time”이 거의 고려되지 못하는 문제가 발생하는 것이다.

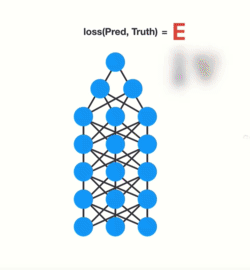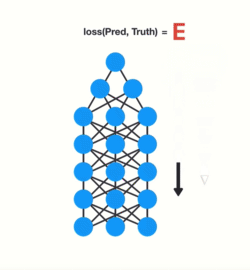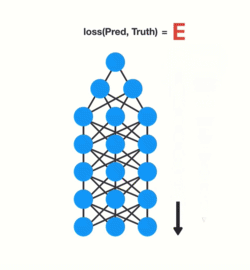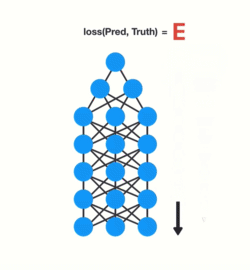
이런 이슈 개선하기 위해서 LSTM(long short term memory)이나 GRU(gated recurrent unit)와 같이 long-term memory를 활용하는 모델/기법이 활용된다. (LSTM과 GRU는 다음 posting에서 다룰 예정)

시계열 예측하기

“What time is it?” 문장과 같이 모든 data가 time step마다 하나 이상의 값을 가진 sequence의 경우 time series(시계열)이라고 부른다. time step마다 하나의 값을 가지는 경우는 univariate(단변량) time series라고 하고, 여러값을 가지는 경우는 multivariate(다변량) time series라고 한다.

time series data를 기반으로 미래를 예측하는 것을 forecasting이라고 부르고, 반대로 과거에 누락되었던 값을 예측하는 것을 imputation(값 대체)라고 한다.

시계열을 다룰때 입력 특성은 일반적으로 크기의 3D 배열로 나타난다. [batch_size, time step수, 차원 수] 단변량 시계열은 dimensionality가 1 이고 다변량 시계열은 1이상이된다. 그래서 단변량인 경우 [batch size, tim step수, 1]크기의 numpy 배열을 반환한다.

기준 성능

각 시계열의 마지막 값을 그대로 예측하는 것을 naive forecasting (순진한 예측)이라고 한다. 이 성능보다 더 좋은 성능을 내는것이 매우 어렵기때문에, naive forecasting의 성능을 기준 성능으로 지정하고 이와 비교해서 모델이 잘 작동하는 지 확인 할 수 있다.

generate_time_series()함수로 시계열 데이터를 생성했다면, 다음과 같이 train, valid, test dataset으로 나누어서 모델 훈련 및 평가를 진행해볼 수 있다.

n_steps = 50
batch_size=10000
#generate_time_series함수로 n_steps길이의 시계열 데이터 생성
series = generate_time_series(10000, n_steps + 1)
X_train, y_train = series[:7000, :n_steps], series[:7000, -1]
X_valid, y_valid = series[7000:9000, :n_steps], series[7000:9000, -1]
X_test, y_test = series[9000:, :n_steps], series[9000:, -1]

y_pred = X_valid[:,-1]
np.mean(keras.losses.mean_squared_error(y_valid, y_pred))
#0.020 수준의 평균제곱오차가 확인된다.

다른 방법으로 다음과 같이 fully connected network을 사용할 수도 있다. 더 좋은 성능의 모델이 만들어지는것을 확인할 수 있다. (mse smaller by an order of magnitude)

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[50,1]),
    keras.layers.Dense(1)
])

model.compile(loss="mse", optimizer="adam")
history = model.fit(X_train, y_train, epochs=20,
                    validation_data=(X_valid, y_valid))

#0.004 수준의 mse가 확인된다.

간단한 RNN (simpleRNN)

위에서 recurrent neuron의 모형으로 보여진것과 같이 simple RNN는하나의 neuron이 있는 하나의 층으로 구성되어있고 기본적으로 활성화 함수로 tanh 함수를 사용한다.

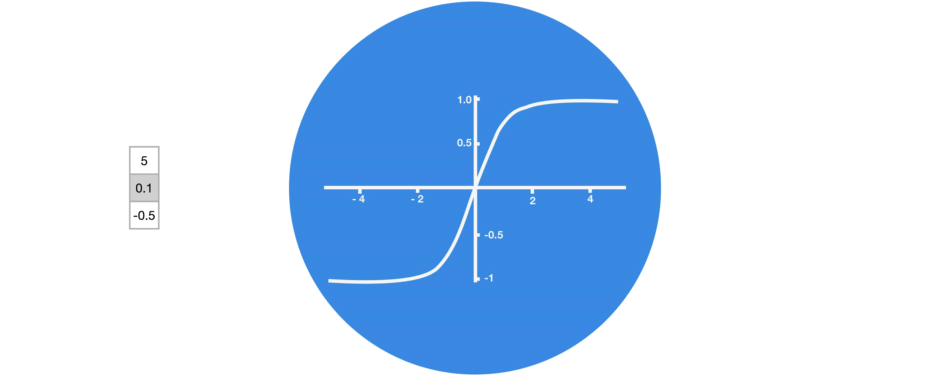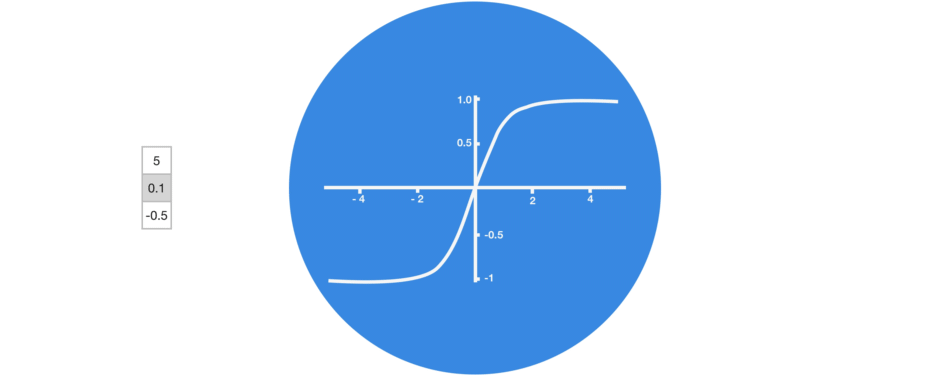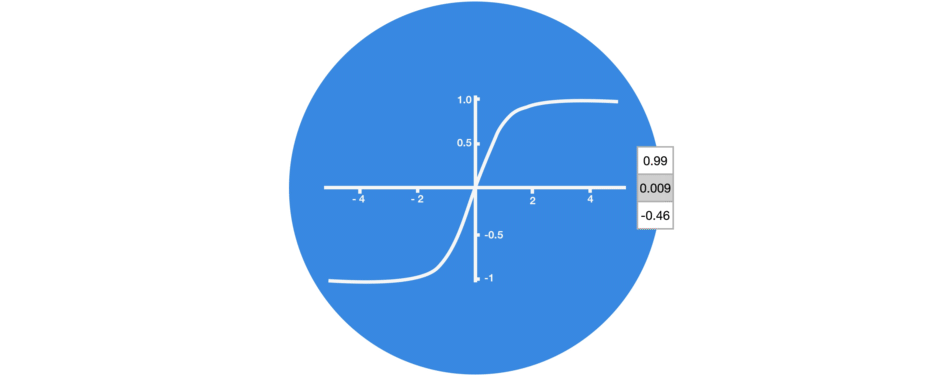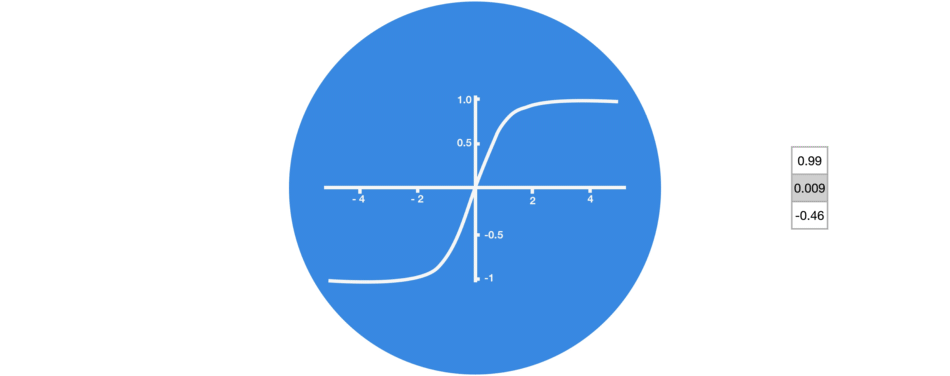
note: tanh을 기본 활성화 함수로 사용하는 이유는? ReLU는 tanh과는 다르게 함수의 ouput 값을 수렴할 수 없기때문에. tanh은 (-1,1) 범위 내로 output값을 수렴해준다. 특히 gradient 소실과 폭주가 우려되는 RNN의 경우에는 tanh과 같은 수렴하는 함수가 필요함.)

다음 그림과 같이 tanh 활성화 함수를 사용하면 출력되는 값을 (-1,1) range로 만든다.

model_simple = keras.models.Sequential([
    #어떤 길이의 time step이든 다 처리하도록 input sequence길이를 설정하지 않는다.
    #그래서 input_shape=[None,1]
    #이 예시의 경우, dataset of num of steps=50가 처리될 것이다.
    keras.layers.SimpleRNN(1, input_shape=[None,1])
])

optimizer = keras.optimizers.Adam(learning_rate=0.005)
model_simple.compile(loss="mse", optimizer=optimizer)
history = model_simple.fit(X_train, y_train, epochs=20,
                    validation_data=(X_valid, y_valid))

#0.011 수준의 mse가 확인된다.

초기 상태 h_init을 0으로 설정하고 첫번째 time step x_0와 함께 하나의 recurrent neuron으로 전달된다. neuron은 이 값의 가중치 합을 계산하고 tanh 활성화 함수를 적용해서 결과를 만들어서 첫번째 y_0를 출력한다. simpleRNN에서는 이 출력이 새로운 상태 h_0이 된다. 그리고 이 새로운 상태는 다음 time step의 입력값인 x_1과 함께 동일한 recurrent neuron으로 전달된다. 이렇게 계속 마지막 time step까지 반복된다. n_step=50의 경우, 마지막 값 y_49를 출력한다.

위에서 fully connected network을 사용했을때에는 (assuming 간단한 linear model) 총 51개의 parameter가 사용한다. (50개의 neuron 각각 하나의 parameter + bias = 51개)

simpleRNN의 경우 recurrent neuron은 입력과 은닉상태 차원 (simpleRNN에서는 neuron수 = 층수) 마다 하나의 parameter를 사용하고 편향이 있기때문에 총 3개의 parameter를 가지고있다. 여기서 확인한 simpleRNN의 성능이 위에서 확인했던 fully connected network의 선형 모델의 mse보다 3배정도 너 높다는것이 확인된다. 어떻게 더 개선할 수 있을까?

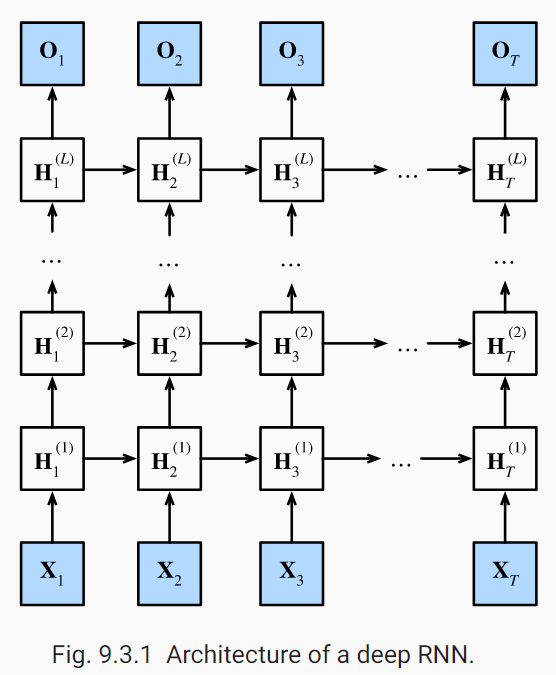
심층 RNN (deepRNN)

일반적으로 RNN은 이렇게 여러 층을 쌓아서 심층RNN으로 활용한다. 모든 순환층헤서 return_sequence=True로 지정하지 않으면, 모든 time step에 대한 출력을 담은 3D 배열이 아니라, 마지막 time step의 출력만 담은 2D 배열을 출력하게되고 다음 순환층이 3D 형태로 sequence를 입력받지 못해서 에러가 발생할 수 있다. 단, 마지막 출력 층과 연결하는 simpleRNN 층에서는 마지막층만 반환되어 dense layer와 연결되도록, return_requence=True를 제거한다.

model_deep = keras.models.Sequential([
    #기본적으로 keras recurrent layer는 최종 출력만 반환하기때문에 step마다 출력을 반환하려면 return_sequences=True로 설정해야함.
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None,1]),
    #tanh이 아닌 다른 활성화 함수 사용하기위해 return_sequences=True제거 후, dense layer를 추가한다.
    #그리고 두번째 simpleRNN 층이 마지막 출력만 반환하도록 return_sequence의 설정X.
    keras.layers.SimpleRNN(20),
    keras.layers.Dense(1) 
])

model_deep.compile(loss="mse", optimizer="adam")
history = model_deep.fit(X_train, y_train, epochs=20,
                    validation_data=(X_valid, y_valid))

#0.003 수준의 mse가 확인된다.

지금까지는 바로 다음 time step의 값을 예측하는 모델을 구현했지만, target을 바꾸어서 여러 time step앞의 값을 예측하도록 만들수 있다.

예를 들어서 10 step앞의 값을 예측하고 싶다면, 바로 다음 time step의 값을 예측하고 이 값을 입력으로 추가해서 더 미래의 값을 예측할 수 있다. 이 보다 더 높은 성능이 확보될 수 있는 방법은 RNN을 훈련하여 다음 값 10개를 한번에 예측하는 것이다. sequence-to-vector 모델을 사용해서 target으로 10개의 값이 담긴 vector를 사용한다.

먼저 target을 다음 10개의 값이 담긴 vector가 되도록 바꾸어야한다.

n_steps = 50
series = generate_time_series(10000, n_steps + 10)
X_train, Y_train = series[:7000, :n_steps], series[:7000, -10:, 0]
X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:, 0]
X_test, Y_test = series[9000:, :n_steps], series[9000:, -10:, 0]

simpleRNN을 적층하면,

model_deep10 = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20),
    #10개의 unit을 가진 출력층
    keras.layers.Dense(10)
])

model_deep10.compile(loss="mse", optimizer="adam")
history = model_deep10.fit(X_train, Y_train, epochs=20,
                    validation_data=(X_valid, Y_valid))

# 0.009 수준의 mse가 확인된다.

여기에서는 마지막 time step에서만 다음 값 10개를 예측하도록 모델을 훈련했지만, 대신 모든 time step에서 다음 값 10개를 예측 하도록 훈련시켜서 성능을 더 개선할 수 있다. 즉,위에서 구현한 sequence-to-vector에서 sequence-to-sequence RNN으로 바꾸는 것이다. 이 방식에서는 마지막 time step에서의 출력 뿐만 아니라 모든 time step에서 RNN 출력에 대한 요소가 loss에 포함된다. 그래서 (시간에 따라서만 흐르는것이 아니라) 더 많은 오차 gradient가 model로 흐르게 된다. 각 time step에서 gradient가 흐를 수 있게되고 이 방식으로 더 안정적이고 빠른 속도로 훈련이 진행될 수 있다.

예를 들면, time step=0에서 model이 time step=1부터 10까지 예측을 담은 vector를 출력한다. 그리고 다음 time step=1에서는 model이 time step=2에서 11까지 예측한다. 각 target은 입력 sequence와 동일한 길이의 sequence이다. 이 sequence는 time step마다 10차원의 vector를 담게된다.

위 모델을 seq2seq로 바꾸기 위해서는 마지막 층을 포함해서 모든 순환층에 return_sequence = True를 지정해야한다. 모든 time step에서의 출력을 Dense층에 적용해야하기때문에, 이를 위해 keras에서 timeDistributed층을 사용한다.

timeDistributed란? timeDistributed는 다른 층을 감싸서 입력 sequence의 모든 time step에 적용되도록 한다.

TimeDistributed layer Keras official doc: https://keras.io/api/layers/recurrent_layers/time_distributed/

model_seq2seq = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20, return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])

timeDistributed층은 각 time step을 별개의 sample처럼 다루도록해서 입력의 크기를 바꾼다. ([batch size, num of time steps, 입력 차원]에서 [batch size x num of time steps, 입력 차원]으로 입력의 크기를 바꿈.) 위 예시의 경우에는 simpleRNN층이 20개의 unit을 가지기 때문에 입력 차원의 길이가 20이다. 그 다음 dense층에 적용한다. 그리고 마지막으로 출력 크기를 sequence로 되돌린다. (출력의 크기를 [batch size x num of time steps, 입력 차원]에서 [batch size, num of time steps, 입력 차원]으로 되돌림.) Dense층이 10개의 unit을 가지기때문에 차원의 길이가 10이다. 개선된 모델을 compile해서 훈련시킨 후 예측성능을 평가해보면 mse가 0.006수준으로 더 개선됬음이 확인된다.

#predict,evaluate을 위해서는 마지막 출력만 있으면되어서 따로 함수를 정의함.
def last_time_step_mse(Y_true, Y_pred):
    return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])

model_seq2seq.compile(loss="mse", optimizer=keras.optimizers.Adam(learning_rate=0.01), metrics=[last_time_step_mse])
history = model_seq2seq.fit(X_train, Y_train, epochs=20,
                    validation_data=(X_valid, Y_valid))

#0.006 수준의 mse가 확인된다.

Reference

1. Geron, Aurelien. Hands on Machine Learning. O’Reilly, 2019
2. RNN explained with illustrations: https://towardsdatascience.com/illustrated-guide-to-recurrent-neural-networks-79e5eb8049c9
3. RNN exaplined in details: https://towardsdatascience.com/learn-how-recurrent-neural-networks-work-84e975feaaf7 / https://medium.com/mindorks/understanding-the-recurrent-neural-network-44d593f112a2