Data Augmentation for TSC

기존 data augmentation techniques

Slicing window

Time series classification 문제에서 기존에 사용된 data augmentation 기법들로는 window slicing, manual warping, 등이 있다.

Times series data에 적용하는 slicing window 기법은 computer vision task에서 image cropping과 비슷하다. Image cropping기반의 data transformation에서는 어느정도는 cropped image에도 original image와 비슷한 정보가 확보된다는 assumption을 세운다. 그러나 time series data에서는 특정 time series region의 cropping으로 분류작업에 중요한 discriminative 정보가 lost되지 않고 포함된다는것이 guarantee되지 못한다. 그래도 time series classification 문제에서 slicing 기법은 종종 사용되어 왔다. (e.g., slicing window technique used to improve SVM accuracy for classifying electroencephalogrpahic time series data as shown in paper “Data Augmentation for Brain-Computer Interfaces: Analysis on Event-Related Potentials Data (2018)”, slicing window technique is also used to improve CNN’s prediction of mortgage deliquency using customers’ historical transactional data in paper “Predicting Mortgage Default Using Convolutional Neural Networks. Exper Systems with Applications(2018)”) Computer vision에서의 일반적인 data augmentation 기법들과 비슷하게 time series data augmentation에서도 jittering, scaling, warping, permutation이 활용될 수 있다.

Time series data에 slicing window 기법을 문제없이 사용하기 위해서는 model이 cropping으로 slice된 각각의 subsequence를 따로 먼저 분류하고 나서 마지막에 전체 time series data를 majority voting approach를 통해 분류하는 과정을 거치는것이 좋다고 한다.

Dynamic Time Warping Barycentric Averaging

Fawaz의 논문에서는 DTW(dynamic time warping) 기법 기반의 DTW Barycentric Averaging (DBA)알고리즘을 사용해서 데이터를 증폭하여 분류성능 개선에 도움이 되는지 실험을 진행했다.

DTW

서로 속도가 다른 두 개의 temporal sequence사이의 similarity를 측정하는 방법이다. 두 개의 time series 사이의 같은/다른점을 matching할 수 있어서 pattern recognition 또는 anomaly detection을 위해서도 활용된다.

DTW는 다음 rule을 기반으로 주어진 sequence들 사이의 optimal match를 구한다.

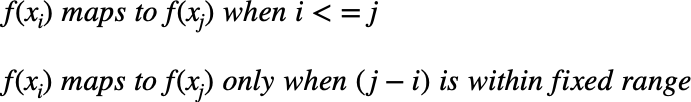
dtw_rule

글로 표현해보면,

first sequence의 모든 index는 second sequence의 one or more indices와 반드시 match되어야 함. and vice versa.
first sequence의 first index는 second sequence의 first index와 반드시 match되어야 함. 반드시 1:1일 필요는 없음. second sequence의 다른 indices와도 match 될 수 있음.
first sequence의 last index는 second sequence의 last index과 반드시 match 되어야 함. 위와 동일하게 1:1일 필요는 없음.
first sequence의 indices가 second sequence의 indices와 mapping되는 관계는 monotonically 증가해야 함. e.g., first sequence의 indices가 j>i라면, second sequence의 indices는 n>m이고, i는 n에, j는 m에 match되어야 함.

DTW를 통해 찾을 수 있는 optimal match는 이 rule들을 모두 만족시키면서 minimal cost를 가지는 match이다. cost는 각각의 match된 pair of indices의 값의 absolute difference를 모두 더한 값으로 계산된다.

간단하게 표현한 문구는 다음과 같다.

“head and tail must be positionally matched, no cross-match and no left-out”

단순한 Euclidean matching은 다음 그림과 같이 매우 restrictive하다.

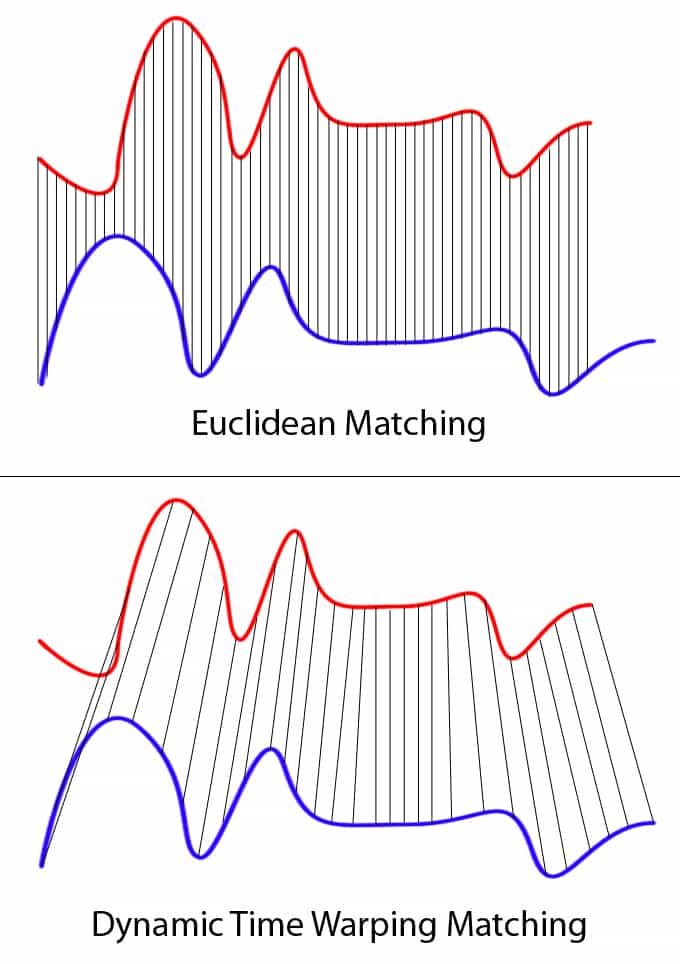
Euclidean vs. DTW

두 series에서 보이는 바와 같이 blue lines으 red line보다 더 길지만, one-to-one match (Euclidean matching)대신에 one-to-many matching(DTW)을 통해 두 lines의 troughs와 peaks가 같은 pattern으로 match될 수 있다.

Python으로 계산하는 방식을 구현해보면,

def dtw(s, t):
    n, m = len(s), len(t)
    dtw_matrix = np.zeros((n+1, m+1))
    for i in range(n+1):
        for j in range(m+1):
            dtw_matrix[i, j] = np.inf
    dtw_matrix[0, 0] = 0
    
    for i in range(1, n+1):
        for j in range(1, m+1):
            cost = abs(s[i-1] - t[j-1])
            # take last min from a square box
            last_min = np.min([dtw_matrix[i-1, j], dtw_matrix[i, j-1], dtw_matrix[i-1, j-1]])
            dtw_matrix[i, j] = cost + last_min
    return dtw_matrix

Matching하려는 sequence가 unlimited number of elements를 가진 경우와 같이 mapping이 매우 심하게 bent over되는 경우는 prevent하기 위해서 다음과 같이 ‘window constraint’를 지정해줄 수 있다.

def dtw(s, t, window):
    n, m = len(s), len(t)
    w = np.max([window, abs(n-m)]) # window constraint
    dtw_matrix = np.zeros((n+1, m+1))
    
    for i in range(n+1):
        for j in range(m+1):
            dtw_matrix[i, j] = np.inf
    dtw_matrix[0, 0] = 0
    
    for i in range(1, n+1):
        for j in range(np.max([1, i-w]), np.min([m, i+w])+1):
            dtw_matrix[i, j] = 0
    
    for i in range(1, n+1):
        for j in range(np.max([1, i-w]), np.min([m, i+w])+1):
            cost = abs(s[i-1] - t[j-1])
            # take last min from a square box
            last_min = np.min([dtw_matrix[i-1, j], dtw_matrix[i, j-1], dtw_matrix[i-1, j-1]])
            dtw_matrix[i, j] = cost + last_min
    return dtw_matrix

fastdtw라는 PyPi library가 있다. 이 library를 import해서 쉽게 matching하려는 두 time series의 distance를 계산할 수 있다.

DTW는 “the optimal alignment between tow time series”를 찾아준다. DTW의 단점 중 하나는 한번에 단 두개의 time series만을 비교할 수 있다는 것이다. 여러개의 time series를 기반으로 comparison을 진행하기위해서는 DTW기반의 DBA(DTW Barycentric Averaging)을 활용할 수 있다.

DBA

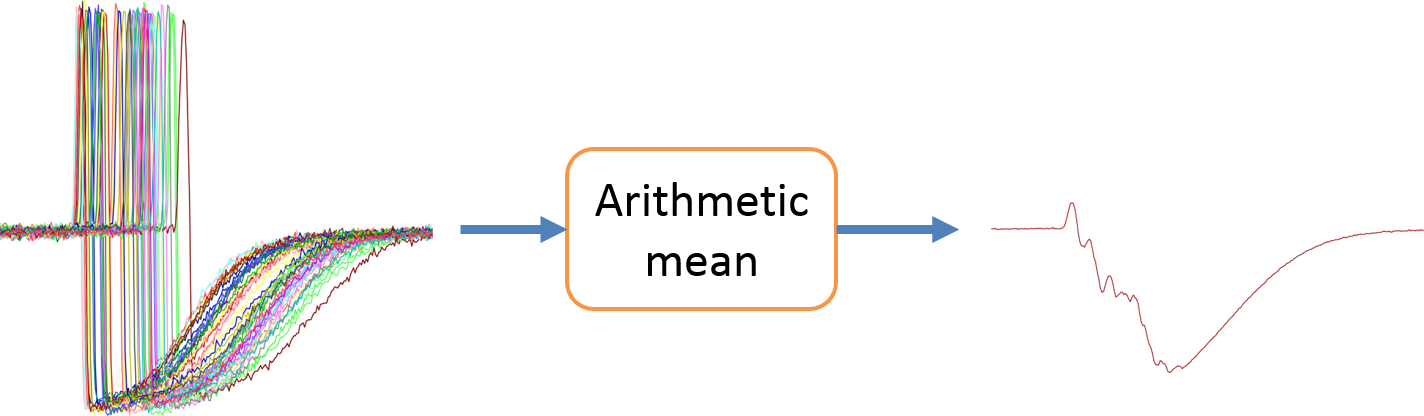
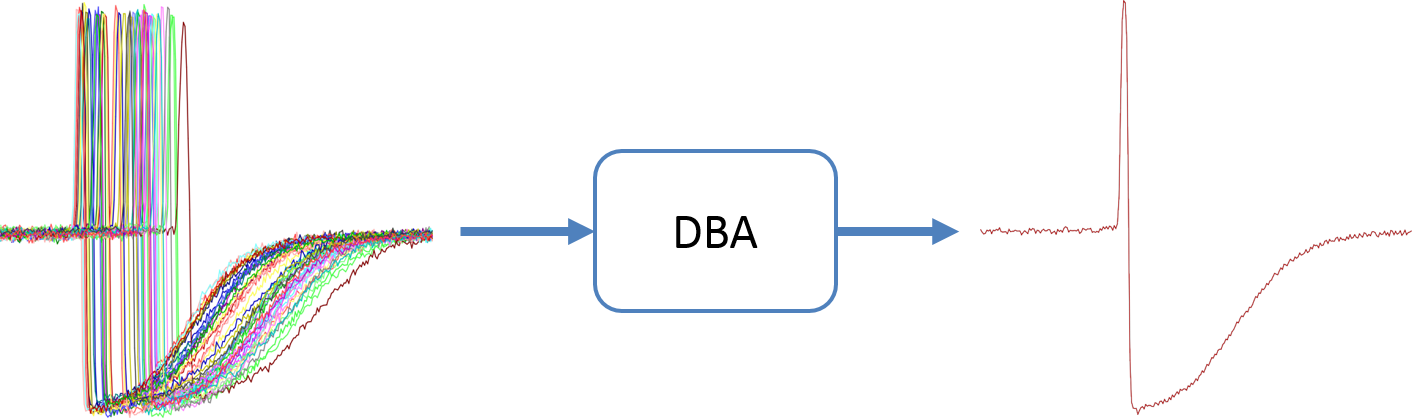
DBA는 최근 data mining에서 많이 활용되고있는 algorithm으로 unlimited number of datasets를 한번에 비교하여서 각 dataset의 key joint features를 표현 할 수 있는 “consensus signal”을 생성해낼 수 있다. 이 논문에서는 DBA를 통해 data augmentation을 위한 synthetic data를 생성해냈다. DBA의 주요 장점은 multiple data streams의 average를 구하되, 이들의 key features를 유지할 수 있다는 점이다.

“tslearn”이라는 time series analysis를 위해 개발된 Python package를 보면, “barycenters”라는 module이 있다. 여기에 dtw_barycenter_averaging() 함수를 통해서 DBA algorithm을 쉽게 구현할 수 있다.

tslearn.barycenters.dtw_barycenter_averaging documentation

multiple time series의 일반적인 arithmetic mean과 DBA를 시각적으로 비교해보면 다음과 같이 차이점이 뚜렷하게 보인다.

arith_mean

DBA

Model

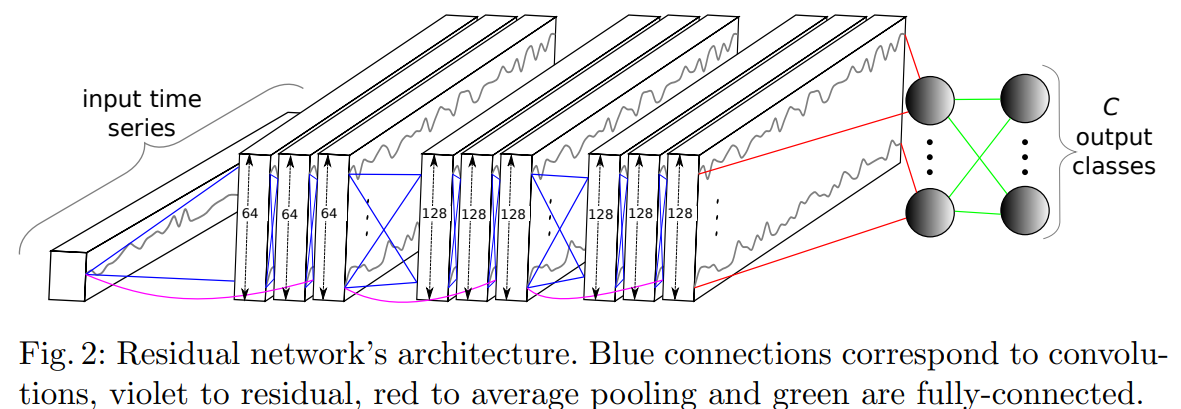
Fawaz의 논문에서는 data augmentation 기법이 분류 task에 얼마나 도움이 되는지 확인하기위해 이미 well-validated된 CNN model인 ResNet을 model architecture로 선택했다.

ResNet 모델 architecture:

ResNet_architecture

ResNet모델의 특징은 residual connection이 gradient들이 convolution과정을 거치지않고 직접적으로 flow되도록 shortcut을 제공하는 것이다.

Model’s input: univariate time series with a varying length l

Model’s output: probability distribution over 분류하려는 C개의 classes

Network’s core: 3 Residual Blocks(each block에는 3개의 1D convolution with filter lengths of 8,5,3이 있고 각각의 convolution은 batch normalization과 ReLU activation function으로 연결되어있음.각각 block들에 순서대로 filter size 64, 128, 128가 적용됨.) + Global Average Pooling + 마지막 softmax classifier

Residual connection: linking input of a residual block to the input of its consecutive layer using addition operation

Data Augmentation

Fawaz가 참고한 논문은 Forestier의 논문 “Generating synthetic time series to augment sparse datasetse (2017)”이다. 참고하는 논문의 DTW Barycentric Averaging (DBA) technique에 varying 가중치를 적용하는 방식을 구현했다. Weighing 방식으로는 Average Selected (selecting a subset of close time series and filling their bounding boxes)가 사용되었다.

Weights가 assign되는 과정은 training set에서 random initial time series를 선택하고 initial weight 0.5를 주어주면서 시작된다. Initial time series의 5 nearest neighbor time series를 DTW를 기반으로 찾고, 이 중에서 random하게 2개를 선택하고 0.15의 weight를 assign한다. 그래서 total sum of assigned weights가 0.5 +(2*0.15) = 0.8이 되도록 한다. Training dataset 전체에서 normalized sum of weights(=1)를 유지하기위해서 나머지 time series들이 나누어 가지는 weights는 0.2로 지정한다.

이렇게 averaging되는 time series에 주어지는 weights를 변경해가면서 원하는 만큼의 synthetic time series dataset을 생성할 수 있다.

Results

DTW와 weighted DBA algorithm기반의 data augmentation을 통해서 UCR time series dataset의 classification accuracy가 크게 개선되는것이 확인되었다. 특히, DiatomSizeReduction이 UCR dataset중에서 가장 사이즈가 작았는데(16개의 training samples밖에 없는데 거의 이 사이즈의 double이 되는 수준의 data augmentation을 진행 함.) classification accuracy가 test했던 UCR dataset들중의 가장 낮은 accuracy인 30%대에서 90%대로 크게 향상된것이 확인되었다. 또한, 1-NN coupled with DTW (Euclidean distance)를 통해 DiatomSizeReduction dataset의 분류성능을 확인해보면 97%수준의 높은 accuracy가 확인된다. 이점은 해당 dataset은 간단한 Euclidean distance만으로 필요한 time series simliarities를 recognize할 수 있다는것을 의미한다. Original training dataset의 sample만으로는 ResNet 모델이 capture할 수없는것을 DTW기반 data augmentation을 통해 capture할 수 있게 된것이다. 이런 개선점은 UCR의 Wine dataset에서도 확인된다.

TSC를 연구하는 community에서 ensemble을 통해 분류 성능을 개선하는 결과를 종종 발표했다. 이점을 활용해서 두개의 ReNet 모델 (one with data augmentation + one without)의 ensemble로 분류성능도 확인한 결과, 전체적인 UCR dataset들을 고려했을때에 분류 accuracy의 개선이 확인되었다. (data augmentation으로 인해 분류 accuracy가 더 나빠지는 dataset의 수가 10개 정도 줄어들었다.)

DTW기반의 data augmentation을 기반으로 생성된 synthetic data를 통해서 CNN모델이 time invariant features를 학습해서 해당 dataset의 분류 성능을 높일 수 있었다.

References

Fawaz, Ismail, et al. Data augmentation using synthetic data for time series classification with deep residual networks (2018)
Forestier, G., Petitjean F., et al. Generating synthetic time series to augment sparse datasets (2017)
corresponding github repository
Wen, Qingsong, et al. Time Series Data Augmentation for Deep Learning: A Survey (2022)
Understanding Dynamic Time Warping by Databricks (https://databricks.com/blog/2019/04/30/understanding-dynamic-time-warping.html)
Dynamic Time Warping: Explanation and Code Implementation by Jeremy Zhang (https://towardsdatascience.com/dynamic-time-warping-3933f25fcdd)

Adventure42

DBA based Data Augmentation for TSC